BlockingQueue
在所有的并发容器中,BlockingQueue是最常见的一种。BlockingQueue是一个带阻塞功能的队列,当入队列时,若队列已满,则阻塞调用者;当出队列时,若队列为空,则阻塞调用者。
在concurrent包中,BlockingQueue是一个接口,有许多个不同的实现类,如图所示。
该接口的定义如下:
public interface BlockingQueue<E> extends Queue<E> {
//...
boolean add(E e);
boolean offer(E e);
void put(E e) throws InterruptedException;
boolean remove(Object o);
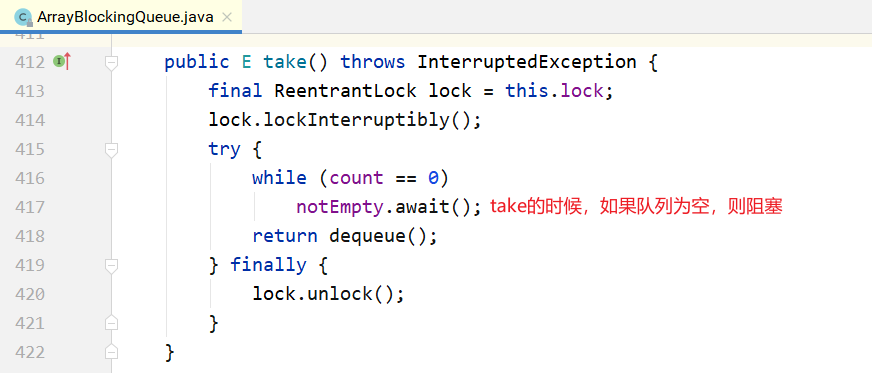
E take() throws InterruptedException;
E poll(long timeout, TimeUnit unit) throws InterruptedException;
//...
}该接口和JDK集合包中的Queue接口是兼容的,同时在其基础上增加了阻塞功能。在这里,入队提供了add(…)、offer(..)、put(…)3个方法,有什么区别呢?从上面的定义可以看到,add(…)和offer(..)的
返回值是布尔类型,而put无返回值,还会抛出中断异常,所以add(…)和offer(..)是无阻塞的,也是Queue本身定义的接口,而put(..)是阻塞的。add(…)和offer(..)的区别不大,当队列为满的时候,前者会抛出异常,后者则直接返回false。
出队列与之类似,提供了remove()、poll()、take()等方法,remove()是非阻塞式的,take()和poll()是阻塞式的。
ArrayBlockingQueue
ArrayBlockingQueue是一个用数组实现的环形队列,在构造方法中,会要求传入数组的容量。
public ArrayBlockingQueue(int capacity) {
this(capacity, false);
}
public ArrayBlockingQueue(int capacity, boolean fair) {
// ...
}
public ArrayBlockingQueue(int capacity, boolean fair, Collection<? extends
E> c) {
this(capacity, fair);
// ...
}其核心数据结构如下:
public class ArrayBlockingQueue<E> extends AbstractQueue<E> implements
BlockingQueue<E>, java.io.Serializable {
//...
final Object[] items;
// 队头指针
int takeIndex;
// 队尾指针
int putIndex;
int count;
// 核心为1个锁外加两个条件
final ReentrantLock lock;
private final Condition notEmpty;
private final Condition notFull;
//...
}其put/take方法也很简单,如下所示:
put方法:
take方法:
LinkedBlockingQueue
LinkedBlockingQueue是一种基于单向链表的阻塞队列。因为队头和队尾是2个指针分开操作的,所以用了2把锁+2个条件,同时有1个AtomicInteger的原子变量记录count数。
public class LinkedBlockingQueue<E> extends AbstractQueue<E> implements
BlockingQueue<E>, java.io.Serializable {
// ...
private final int capacity;
// 原子变量
private final AtomicInteger count = new AtomicInteger(0);
// 单向链表的头部
private transient Node<E> head;
// 单向链表的尾部
private transient Node<E> last;
// 两把锁,两个条件
private final ReentrantLock takeLock = new ReentrantLock();
private final Condition notEmpty = takeLock.newCondition();
private final ReentrantLock putLock = new ReentrantLock();
private final Condition notFUll = putLock.newCondition();
// ...
}在其构造方法中,也可以指定队列的总容量。如果不指定,默认为Integer.MAX_VALUE。

put/take实现:

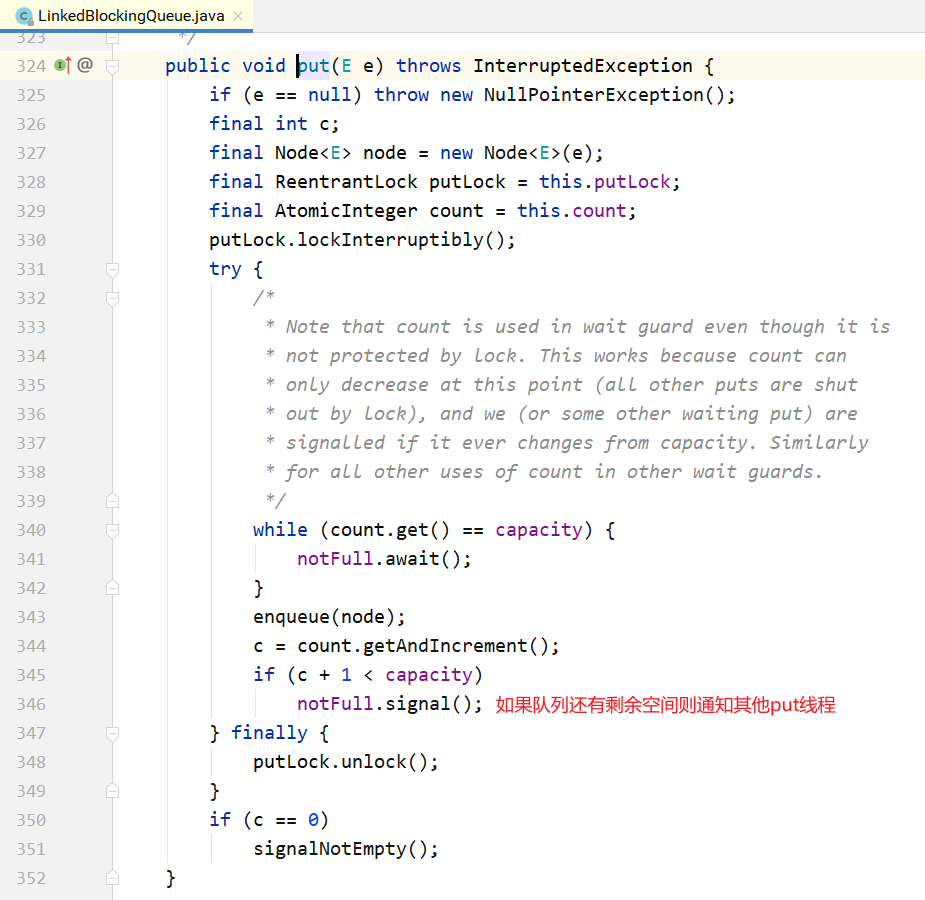
LinkedBlockingQueue和ArrayBlockingQueue的差异:
- 为了提高并发度,用2把锁,分别控制队头、队尾的操作。意味着在
put(…)和put(…)之间、take()与take()之间是互斥的,put(…)和take()之间并不互斥。但对于count变量,双方都需要操作,所以必须是原子类型 - 因为各自拿了一把锁,所以当需要调用对方的
Condition的signal时,还必须再加上对方的锁,就是signalNotEmpty()和signalNotFull()方法。示例如下所示:
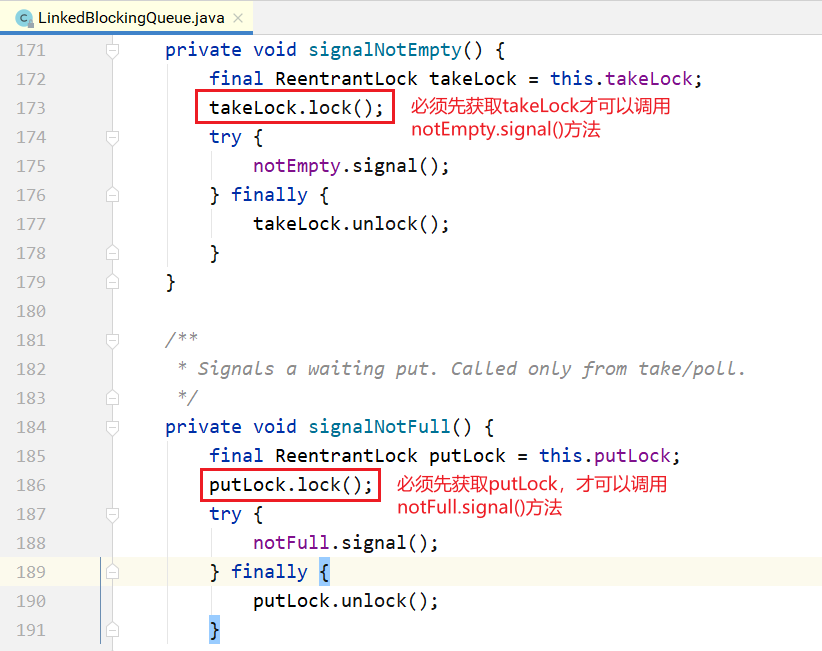
- 不仅
put会通知take,take也会通知put。当put发现非满的时候,也会通知其他put线程;当take发现非空的时候,也会通知其他take线程
PriorityBlockingQueue
队列通常是先进先出的,而PriorityQueue是按照元素的优先级从小到大出队列的。正因为如此,PriorityQueue中的2个元素之间需要可以比较大小,并实现Comparable接口。
其核心数据结构如下:
public class PriorityBlockingQueue<E> extends AbstractQueue<E> implements
BlockingQueue<E>, java.io.Serializable {
//...
// 用数组实现的二插小顶堆
private transient Object[] queue;
private transient int size;
private transient Comparator<? super E> comparator;
// 1个锁+一个条件,没有非满条件
private final ReentrantLock lock;
private final Condition notEmpty;
//...
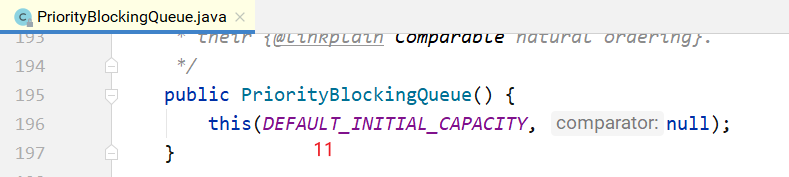
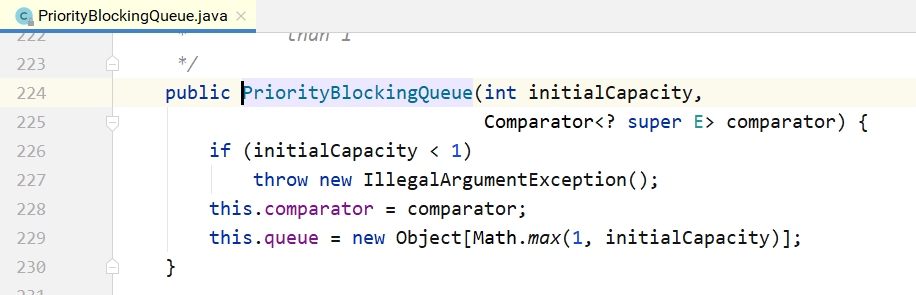
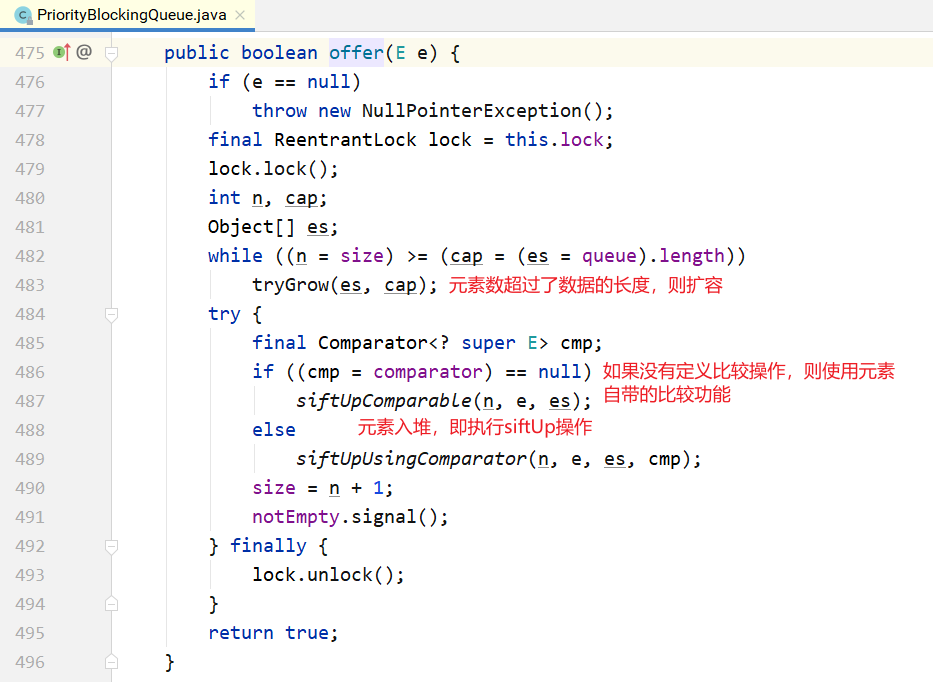
}其构造方法如下所示,如果不指定初始大小,内部会设定一个默认值11,当元素个数超过这个大小之后,会自动扩容。

下面是对应的put/take方法的实现。
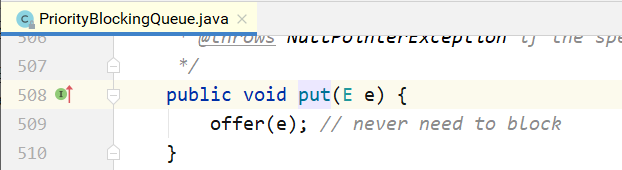
put方法的实现:
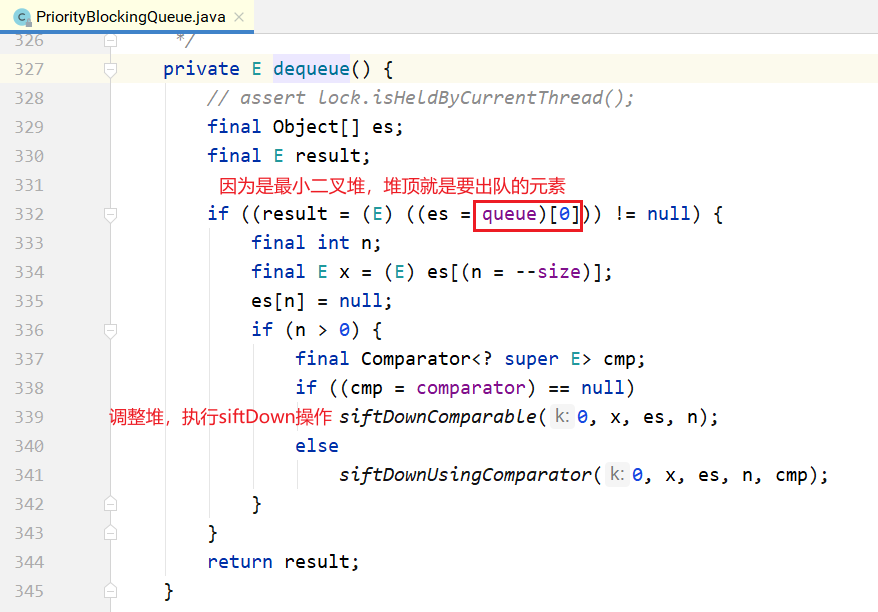
take的实现:
从上面可以看到,在阻塞的实现方面,和ArrayBlockingQueue的机制相似,主要区别是用数组实现了一个二叉堆,从而实现按优先级从小到大出队列。另一个区别是没有notFull条件,当元素个数超出数组长度时,执行扩容操作。
DelayQueue
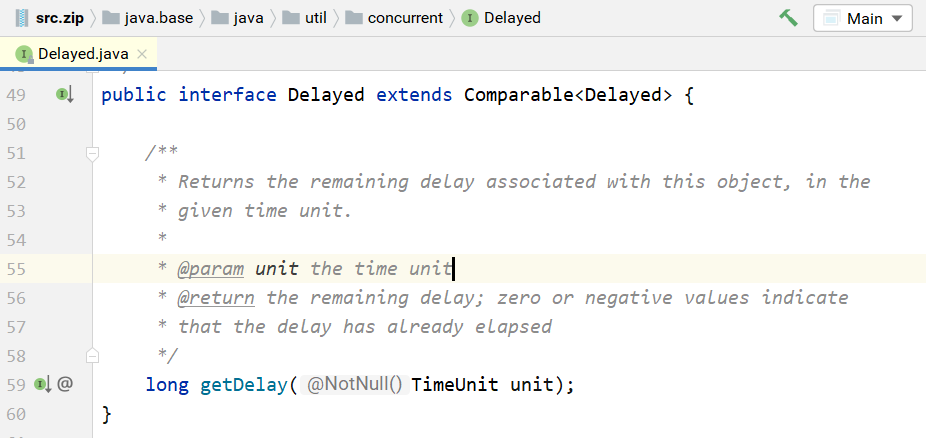
DelayQueue即延迟队列,也就是一个按延迟时间从小到大出队的PriorityQueue。所谓延迟时间,就是“未来将要执行的时间”减去“当前时间”。为此,放入DelayQueue中的元素,必须实现Delayed接口,如下所示:
关于该接口:
- 如果
getDelay的返回值小于或等于0,则说明该元素到期,需要从队列中拿出来执行 - 该接口首先继承了
Comparable接口,所以要实现该接口,必须实现Comparable接口。具体来说,就是基于getDelay()的返回值比较两个元素的大小
下面看一下DelayQueue的核心数据结构:
public class DelayQueue<E extends Delayed> extends AbstractQueue<E>
implements BlockingQueue<E> {
// ...
// 一把锁和一个非空条件
private final transient ReentrantLock lock = new ReentrantLock();
private final Condition available = lock.newCondition();
// 优先级队列
private final PriorityQueue<E> q = new PriorityQueue<E>();
// ...
}下面介绍put/take的实现,先从take说起,因为这样更能看出DelayQueue的特性。
关于take()方法:
- 不同于一般的阻塞队列,只在队列为空的时候,才阻塞。如果堆顶元素的延迟时间没到,也会阻塞
- 在上面的代码中使用了一个优化技术,用一个
Thread leader变量记录了等待堆顶元素的第1个线程。为什么这样做呢?通过getDelay(..)可以知道堆顶元素何时到期,不必无限期等待,可以使用Condition.awaitNanos()等待一个有限的时间;只有当发现还有其他线程也在等待堆顶元素(leader != null)时,才需要无限期等待
put()的实现:


注意:不是每放入一个元素,都需要通知等待的线程。放入的元素,如果其延迟时间大于当前堆顶的元素延迟时间,就没必要通知等待的线程;只有当延迟时间是最小的,在堆顶时,才有必要通知等待的线程,也就是上面代码中的部分。
SynchronousQueue
SynchronousQueue是一种特殊的BlockingQueue,它本身没有容量。先调put(…),线程会阻塞;直到另外一个线程调用了take(),两个线程才同时解锁,反之亦然。
接下来看SynchronousQueue的实现。
构造方法:

和锁一样,也有公平和非公平模式。如果是公平模式,则用TransferQueue实现;如果是非公平模式,则用TransferStack实现。这两个类分别是什么呢?先看一下put/take的实现:
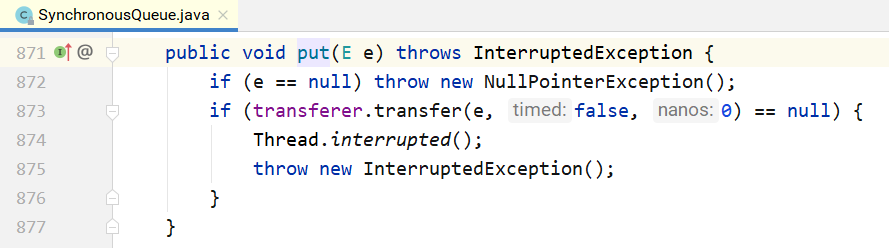
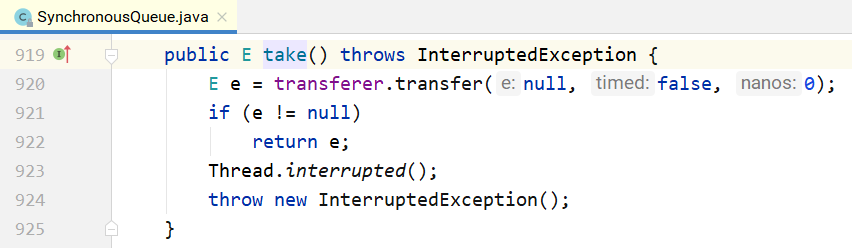
可以看到,put/take都调用了transfer(…)接口。而TransferQueue和TransferStack分别实现了这个接口。该接口在SynchronousQueue内部,如下所示。如果是put(…),则第1个参数就是对应的元素;如果是take(),则第1个参数为null。后2个参数分别为是否设置超时和对应的超时时间。

接下来看一下什么是公平模式和非公平模式。假设3个线程分别调用了put(…),3个线程会进入阻塞状态,直到其他线程调用3次take(),和3个put(…)一一配对。
如果是公平模式(队列模式),则第1个调用put(…)的线程1会在队列头部,第1个到来的take()线程和它进行配对,遵循先到先配对的原则,所以是公平的;如果是非公平模式(栈模式),则第3个调用put(…)的线程3会在栈顶,第1个到来的take()线程和它进行配对,遵循的是后到先配对的原则,所以是非公平的。
下面分别看一下TransferQueue和TransferStack的实现。
TransferQueue
public class SynchronousQueue<E> extends AbstractQueue<E> implements
BlockingQueue<E>, java.io.Serializable {
// ...
static final class TransferQueue<E> extends Transferer<E> {
static final class QNode {
volatile QNode next;
volatile Object item;
volatile Thread waiter;
final boolean isData;
//...
}
transient volatile QNode head;
transient volatile QNode tail;
// ...
}
}从上面的代码可以看出,TransferQueue是一个基于单向链表而实现的队列,通过head和tail2个指针记录头部和尾部。初始的时候,head和tail会指向一个空节点,构造方法如下所示:

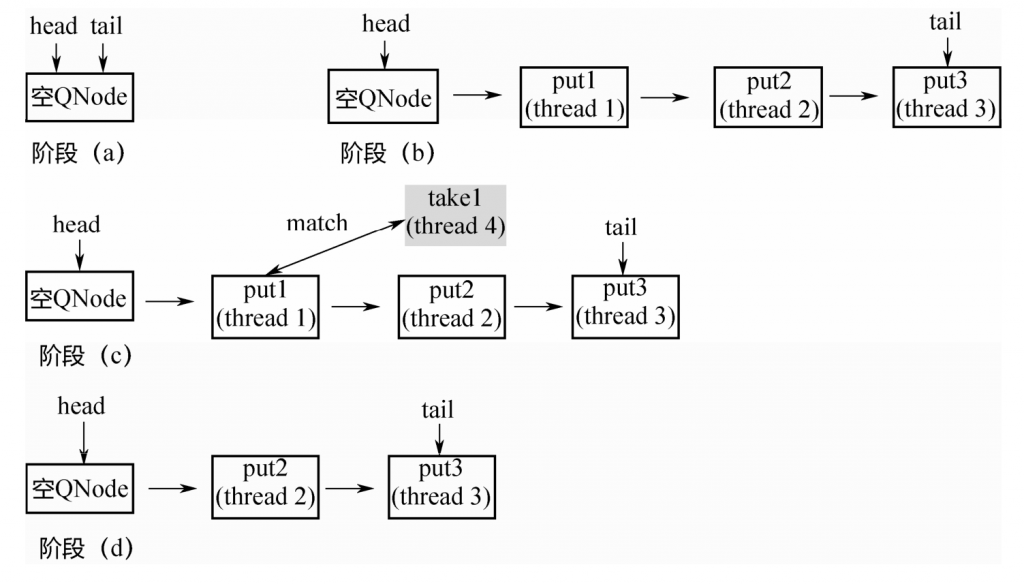
阶段(a):队列中是一个空的节点,head/tail都指向这个空节点。
阶段(b):3个线程分别调用put,生成3个QNode,进入队列。
阶段(c):来了一个线程调用take,会和队列头部的第1个QNode进行配对。
阶段(d):第1个QNode出队列。
这里有一个关键点:put节点和take节点一旦相遇,就会配对出队列,所以在队列中不可能同时存在put节点和take节点,要么所有节点都是put节点,要么所有节点都是take节点。
接下来看一下TransferQueue的代码实现。

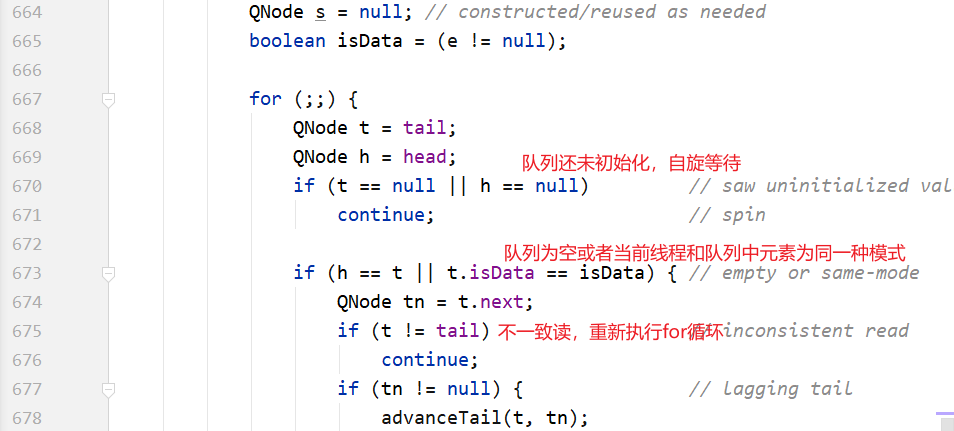


整个for循环有两个大的if-else分支,如果当前线程和队列中的元素是同一种模式(都是put节点或者take节点),则与当前线程对应的节点被加入队列尾部并且阻塞;如果不是同一种模式,则选取队列头部的第1个元素进行配对。
这里的配对就是m.casItem(x,e),把自己的item x换成对方的item e,如果CAS操作成功,则配对成功。如果是put节点,则isData=true,item!=null;如果是take节点,则isData=false,item=null。如果CAS操作不成功,则isData和item之间将不一致,也就是isData!=(x!=null),通过这个条件可以判断节点是否已经被匹配过了。
TransferStack
TransferStack的定义如下所示,首先,它也是一个单向链表。不同于队列,只需要head指针就能实现入栈和出栈操作。
static final class TransferStack extends Transferer {
static final int REQUEST = 0;
static final int DATA = 1;
static final int FULFILLING = 2;
static final class SNode {
volatile SNode next; // 单向链表
volatile SNode match; // 配对的节点
volatile Thread waiter; // 对应的阻塞线程
Object item;
int mode; // 三种模式
//...
}
volatile SNode head;
}链表中的节点有三种状态,REQUEST对应take节点,DATA对应put节点,二者配对之后,会生成一个FULFILLING节点,入栈,然后FULLING节点和被配对的节点一起出栈。
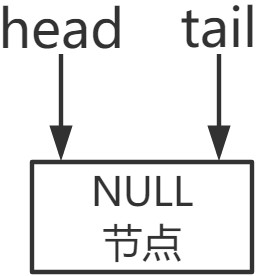
阶段(a):head指向NULL。不同于TransferQueue,这里没有空的头节点。
阶段(b):3个线程调用3次put,依次入栈。
阶段(c):线程4调用take,和栈顶的第1个元素配对,生成FULLFILLING节点,入栈。
阶段(d):栈顶的2个元素同时出栈。
下面看一下具体的代码实现:




BlockingDeque
BlockingDeque定义了一个阻塞的双端队列接口,如下所示:
public interface BlockingDeque<E> extends BlockingQueue<E>, Deque<E> {
void putFirst(E e) throws InterruptedException;
void putLast(E e) throws InterruptedException;
E takeFirst() throws InterruptedException;
E takeLast() throws InterruptedException;
// ...
}该接口继承了BlockingQueue接口,同时增加了对应的双端队列操作接口。该接口只有一个实现,就是LinkedBlockingDeque。
其核心数据结构如下所示,是一个双向链表:
public class LinkedBlockingDeque<E> extends AbstractQueue<E> implements
BlockingDeque<E>, java.io.Serializable {
static final class Node<E> {
E item;
Node<E> prev; // 双向链表的Node
Node<E> next;
Node(E x) {
item = x;
}
}
transient Node<E> first; // 队列的头和尾
transient Node<E> last;
private transient int count; // 元素个数
private final int capacity; // 容量
// 一把锁+两个条件
final ReentrantLock lock = new ReentrantLock();
private final Condition notEmpty = lock.netCondition();
private final Condition notFull = lock.newCondition();
// ...
}对应的实现原理,和LinkedBlockingQueue基本一样,只是LinkedBlockingQueue是单向链表,而LinkedBlockingDeque是双向链表。




CopyOnWrite
CopyOnWrite指在“写”的时候,不是直接“写”源数据,而是把数据拷贝一份进行修改,再通过悲观锁或者乐观锁的方式写回。
那为什么不直接修改,而是要拷贝一份修改呢?
这是为了在“读”的时候不加锁。
CopyOnWriteArrayList
和ArrayList一样,CopyOnWriteArrayList的核心数据结构也是一个数组,代码如下:
public class CopyOnWriteArrayList<E> implements List<E>, RandomAccess,
Cloneable, java.io.Serializable {
// ...
private volatile transient Object[] array;
}下面是CopyOnArrayList的几个“读”方法:
final Object[] getArray() {
return array;
}
public E get(int index) {
return elementAt(getArray(), index);
}
public boolean isEmpty() {
return size() == 0;
}
public boolean contains(Object o) {
return indexOf(o) >= 0;
}
public int indexOf(Object o) {
Object[] es = getArray();
return indexOfRange(o, es, 0, es.length);
}
private static int indexOfRange(Object o, Object[] es, int from, int to)
{
if (o == null) {
for (int i = from; i < to; i++)
if (es[i] == null)
return i;
} else {
for (int i = from; i < to; i++)
if (o.equals(es[i]))
return i;
}
return -1;
}既然这些“读”方法都没有加锁,那么是如何保证“线程安全”呢?答案在“写”方法里面。
public class CopyOnWriteArrayList<E>
implements List<E>, RandomAccess, Cloneable, java.io.Serializable {
// 锁对象
final transient Object lock = new Object();
public boolean add(E e) {
synchronized (lock) { // 同步锁对象
Object[] es = getArray();
int len = es.length;
es = Arrays.copyOf(es, len + 1); // CopyOnWrite,写的时候,先拷贝一
份之前的数组
es[len] = e;
setArray(es);
return true;
}
}
public void add(int index, E element) {
synchronized (lock) { // 同步锁对象
Object[] es = getArray();
int len = es.length;
if (index > len || index < 0)
throw new IndexOutOfBoundsException(outOfBounds(index,
len));
Object[] newElements;
int numMoved = len - index;
if (numMoved == 0)
newElements = Arrays.copyOf(es, len + 1);
else {
newElements = new Object[len + 1];
System.arraycopy(es, 0, newElements, 0, index); //
CopyOnWrite,写的时候,先拷贝一份之前的数组
System.arraycopy(es, index, newElements, index + 1,
numMoved);
}
newElements[index] = element;
setArray(newElements); // 把新数组赋值给老数组
}
}
}其他“写”方法,例如remove和add类似,此处不再详述。
CopyOnWriteArraySet
CopyOnWriteArraySet就是用Array实现的一个Set,保证所有元素都不重复。其内部是封装的一个CopyOnWriteArrayList。
public class CopyOnWriteArraySet<E> extends AbstractSet<E> implements
java.io.Serializable {
// 新封装的CopyOnWriteArrayList
private final CopyOnWriteArrayList<E> al;
public CopyOnWriteArraySet() {
al = new CopyOnWriteArrayList<E>();
}
public boolean add(E e) {
return al.addIfAbsent(e); // 不重复的加进去
}
}ConcurrentLinkedQueue/Deque
AQS内部的阻塞队列实现原理:基于双向链表,通过对head/tail进行CAS操作,实现入队和出队。
ConcurrentLinkedQueue的实现原理和AQS内部的阻塞队列类似:同样是基于CAS,同样是通过head/tail指针记录队列头部和尾部,但还是有稍许差别。
首先,它是一个单向链表,定义如下:
public class ConcurrentLinkedQueue<E> extends AbstractQueue<E> implements
Queue<E>, java.io.Serializable {
private static class Node<E> {
volatile E item;
volatile Node<E> next;
//...
}
private transient volatile Node<E> head;
private transient volatile Node<E> tail;
//...
}其次,在AQS的阻塞队列中,每次入队后,tail一定后移一个位置;每次出队,head一定后移一个位置,以保证head指向队列头部,tail指向链表尾部。
但在ConcurrentLinkedQueue中,head/tail的更新可能落后于节点的入队和出队,因为它不是直接对head/tail指针进行 CAS操作的,而是对Node中的item进行操作。下面进行详细分析:
初始化:
初始的时候,head和tail都指向一个null节点。对应的代码如下:
public ConcurrentLinkedQueue() {
head = tail = new Node<E>(null);
}入队列:
代码如下所示:
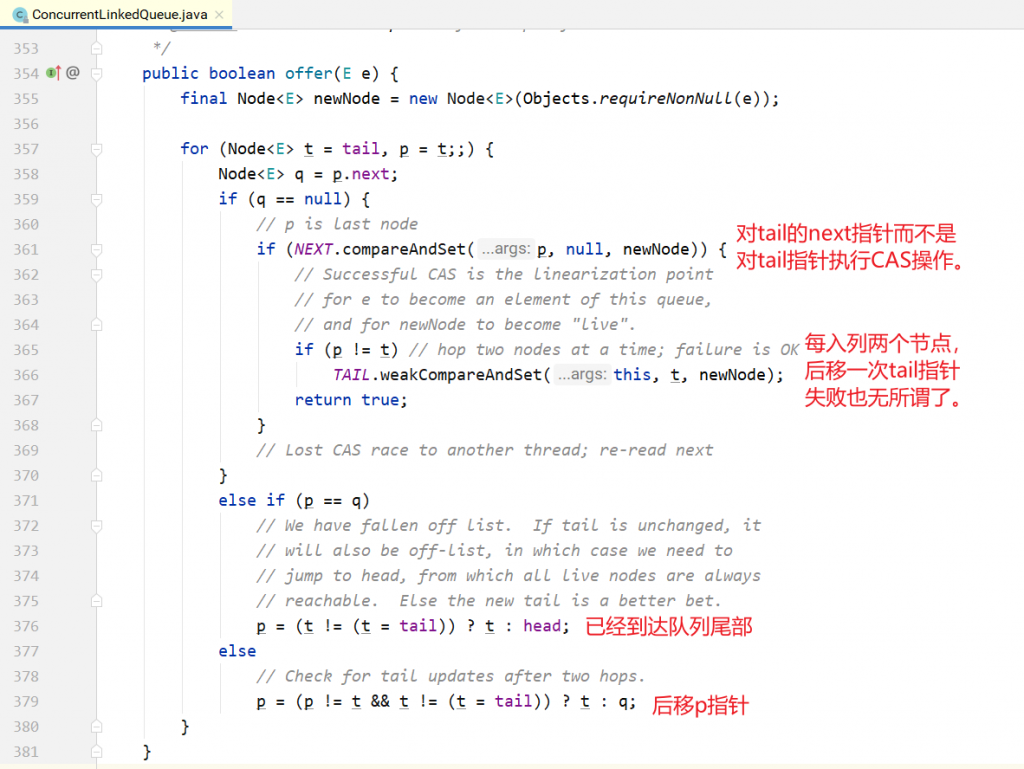
上面的入队其实是每次在队尾追加2个节点时,才移动一次tail节点。如下图所示:
初始的时候,队列中有1个节点item1,tail指向该节点,假设线程1要入队item2节点:
step1:p=tail,q=p.next=NULL
step2:对p的next执行CAS操作,追加item2,成功之后,p=tail。所以上面的casTail方法不会执行,直接返回。此时tail指针没有变化
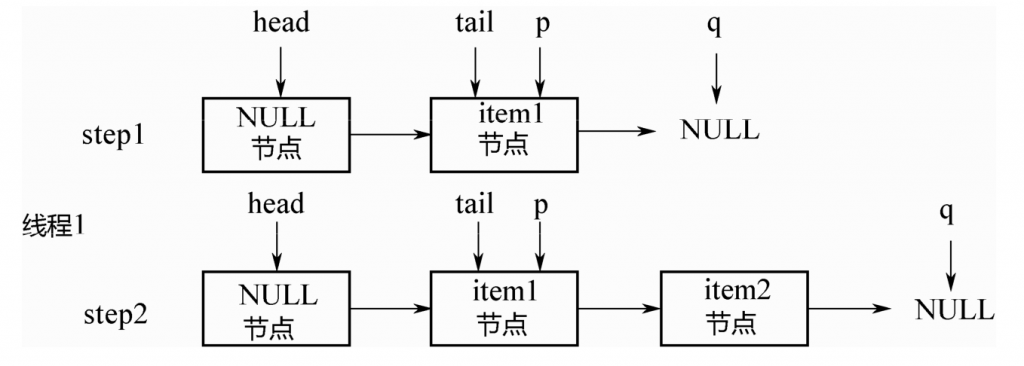
之后,假设线程2要入队item3节点,如下图所示:
step3:p=tail,q=p.next
step4:q!=null,因此不会入队新节点。p,q都后移1位
step5:q=null,对p的next执行CAS操作,入队item3节点
step6:p!=t,满足条件,执行上面的casTail操作,tail后移2个位置,到达队列尾部
最后总结一下入队列的两个关键点:
- 即使
tail指针没有移动,只要对p的next指针成功进行CAS操作,就算成功入队列 - 只有当
p != tail的时候,才会后移tail指针。也就是说,每连续追加2个节点,才后移1次tail指针。即使CAS失败也没关系,可以由下1个线程来移动tail指针
出队列:
上面说了入队列之后,tail指针不变化,那是否会出现入队列之后,要出队列却没有元素可出的情况呢?

出队列的代码和入队列类似,也有p、q2个指针,整个变化过程如图所示。假设初始的时候head指向空节点,队列中有item1、item2、item3 三个节点。
step1:p=head,q=p.next,p!=q
step2:后移p指针,使得p=q
step3:出队列。关键点:此处并没有直接删除item1节点,只是把该节点的item通过CAS操作置为了null
step4:p!=head,此时队列中有了2个null节点,再前移1次head指针,对其执行updateHead操作

最后总结一下出队列的关键点:
- 出队列的判断并非观察
tail指针的位置,而是依赖于head指针后续的节点是否为null这一条件 - 只要对节点的item执行CAS操作,置为null成功,则出队列成功。即使
head指针没有成功移动,也可以由下1个线程继续完成
队列判空:
因为head/tail并不是精确地指向队列头部和尾部,所以不能简单地通过比较head/tail指针来判断队列是否为空,而是需要从head指针开始遍历,找第1个不为null的节点。如果找到,则队列不为空;如果找不到,则队列为空。代码如下所示:


ConcurrentHashMap
HashMap通常的实现方式是“数组+链表”,这种方式被称为“拉链法”。ConcurrentHashMap在这个基本原理之上进行了各种优化。
首先是所有数据都放在一个大的HashMap中;其次是引入了红黑树。
其原理如下图所示:

如果头节点是Node类型,则尾随它的就是一个普通的链表;如果头节点是TreeNode类型,它的后面就是一颗红黑树,TreeNode是Node的子类。
链表和红黑树之间可以相互转换:初始的时候是链表,当链表中的元素超过某个阈值时,把链表转换成红黑树;反之,当红黑树中的元素个数小于某个阈值时,再转换为链表。
那为什么要做这种设计呢?
- 使用红黑树,当一个槽里有很多元素时,其查询和更新速度会比链表快很多,Hash冲突的问题由此得到较好的解决
- 加锁的粒度,并非整个
ConcurrentHashMap,而是对每个头节点分别加锁,即并发度,就是Node数组的长度,初始长度为16 - 并发扩容,这是难度最大的。当一个线程要扩容
Node数组的时候,其他线程还要读写,因此处理过程很复杂,后面会详细分析
由上述对比可以总结出来:这种设计一方面降低了Hash冲突,另一方面也提升了并发度。
下面从构造方法开始,一步步深入分析其实现过程。
构造方法分析:

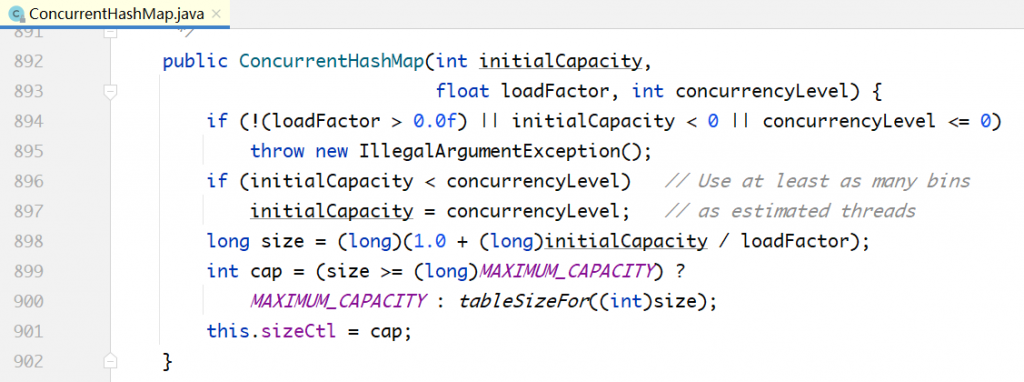
在上面的代码中,变量cap就是Node数组的长度,保持为2的整数次方。tableSizeFor(…)方法是根据传入的初始容量,计算出一个合适的数组长度。具体而言:1.5倍的初始容量+1,再往上取最接近的2的整数次方,作为数组长度cap的初始值。
这里的sizeCtl,其含义是用于控制在初始化或者并发扩容时候的线程数,只不过其初始值设置成cap。
初始化:
在上面的构造方法里只计算了数组的初始大小,并没有对数组进行初始化。当多个线程都往里面放入元素的时候,再进行初始化。这就存在一个问题:多个线程重复初始化。下面看一下是如何处理的:
private final Node<K,V>[] initTable() {
Node<K,V>[] tab; int sc;
while ((tab = table) == null || tab.length == 0) {
if ((sc = sizeCtl) < 0)
Thread.yield(); // 自旋等待
else if (U.compareAndSetInt(this, SIZECTL, sc, -1)) { // 重点:将
sizeCtl设置为-1
try {
if ((tab = table) == null || tab.length == 0) {
int n = (sc > 0) ? sc : DEFAULT_CAPACITY;
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; // 初始化
table = tab = nt;
// sizeCtl不是数组长度,因此初始化成功后,就不再等于数组长度
// 而是n-(n>>>2)=0.75n,表示下一次扩容的阈值:n-n/4
sc = n - (n >>> 2);
}
} finally {
sizeCtl = sc; // 设置sizeCtl的值为sc
}
break;
}
}
return tab;
}通过上面的代码可以看到,多个线程的竞争是通过对sizeCtl进行CAS操作实现的。如果某个线程成功地把sizeCtl设置为-1,它就拥有了初始化的权利,进入初始化的代码模块,等到初始化完成,再把sizeCtl设置回去;其他线程则一直执行while循环,自旋等待,直到数组不为null,即当初始化结束时,退出整个方法。
因为初始化的工作量很小,所以此处选择的策略是让其他线程一直等待,而没有帮助其初始化。
put(..)实现分析:
/**
* Maps the specified key to the specified value in this table.
* Neither the key nor the value can be null.
*
* <p>The value can be retrieved by calling the {@code get} method
* with a key that is equal to the original key.
*
* @param key key with which the specified value is to be associated
* @param value value to be associated with the specified key
* @return the previous value associated with {@code key}, or
* {@code null} if there was no mapping for {@code key}
* @throws NullPointerException if the specified key or value is null
*/
public V put(K key, V value) {
return putVal(key, value, false);
}final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node<K,V> e = f;; ++binCount) {
K ek;
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
Node<K,V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
else if (f instanceof TreeBin) {
Node<K,V> p;
binCount = 2;
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
addCount(1L, binCount);
return null;
}上面的for循环有4个大的分支:
- 第1个分支,是整个数组的初始化
- 第2个分支,是所在的槽为空,说明该元素是该槽的第一个元素,直接新建一个头节点,然后返回
- 第3个分支,说明该槽正在进行扩容,帮助其扩容
- 第4个分支,就是把元素放入槽内。槽内可能是一个链表,也可能是一棵红黑树,通过头节点的类型可以判断是哪一种。第4个分支是包裹在
synchronized(f)里面的,f对应的数组下标位置的头节点,意味着每个数组元素有一把锁,并发度等于数组的长度
上面的binCount表示链表的元素个数,当这个数目超过TREEIFY_THRESHOLD=8时,把链表转换成红黑树,也就是 treeifyBin(tab, i)方法。但在这个方法内部,不一定需要进行红黑树转换,可能只做扩容操作,所以接下来从扩容看起。
扩容:
扩容的实现是最复杂的,下面从treeifyBin(Node[] tab, int index)看起。
/**
* Replaces all linked nodes in bin at given index unless table is
* too small, in which case resizes instead.
*/
private final void treeifyBin(Node<K,V>[] tab, int index) {
Node<K,V> b; int n, sc;
if (tab != null) {
if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
// 数组长度小于阈值64,不做红黑树转换,直接扩容
tryPresize(n << 1);
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
synchronized (b) {
if (tabAt(tab, index) == b) {
TreeNode<K,V> hd = null, tl = null;
for (Node<K,V> e = b; e != null; e = e.next) {
TreeNode<K,V> p =
new TreeNode<K,V>(e.hash, e.key, e.val,
null, null);
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p;
tl = p;
}
setTabAt(tab, index, new TreeBin<K,V>(hd));
}
}
}
}
}在上面的代码中,MIN_TREEIFY_CAPACITY=64,意味着当数组的长度没有超过64的时候,数组的每个节点里都是链表,只会扩容,不会转换成红黑树。只有当数组长度大于或等于64时,才考虑把链表转换成红黑树。
在tryPresize(int size)内部调用了一个核心方法transfer(Node<K,V>[] tab,Node<K,V>[] nextTab),先从这个方法的分析说起。
/**
* Moves and/or copies the nodes in each bin to new table. See
* above for explanation.
*/
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
int n = tab.length, stride;
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE; // subdivide range
if (nextTab == null) { // initiating
try {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
nextTab = nt;
} catch (Throwable ex) { // try to cope with OOME
sizeCtl = Integer.MAX_VALUE;
return;
}
nextTable = nextTab;
transferIndex = n;
}
int nextn = nextTab.length;
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
boolean advance = true;
boolean finishing = false; // to ensure sweep before committing nextTab
for (int i = 0, bound = 0;;) {
Node<K,V> f; int fh;
while (advance) {
int nextIndex, nextBound;
if (--i >= bound || finishing)
advance = false;
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
else if (U.compareAndSwapInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ?
nextIndex - stride : 0))) {
bound = nextBound;
i = nextIndex - 1;
advance = false;
}
}
if (i < 0 || i >= n || i + n >= nextn) {
int sc;
if (finishing) {
nextTable = null;
table = nextTab;
sizeCtl = (n << 1) - (n >>> 1);
return;
}
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
return;
finishing = advance = true;
i = n; // recheck before commit
}
}
else if ((f = tabAt(tab, i)) == null)
advance = casTabAt(tab, i, null, fwd);
else if ((fh = f.hash) == MOVED)
advance = true; // already processed
else {
synchronized (f) {
if (tabAt(tab, i) == f) {
Node<K,V> ln, hn;
if (fh >= 0) {
int runBit = fh & n;
Node<K,V> lastRun = f;
for (Node<K,V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {
ln = lastRun;
hn = null;
}
else {
hn = lastRun;
ln = null;
}
for (Node<K,V> p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
else if (f instanceof TreeBin) {
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> lo = null, loTail = null;
TreeNode<K,V> hi = null, hiTail = null;
int lc = 0, hc = 0;
for (Node<K,V> e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode<K,V> p = new TreeNode<K,V>
(h, e.key, e.val, null, null);
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
(hc != 0) ? new TreeBin<K,V>(lo) : t;
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
(lc != 0) ? new TreeBin<K,V>(hi) : t;
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
}
}
}
}
}该方法非常复杂,下面一步步分析:
- 扩容的基本原理如下图,首先建一个新的
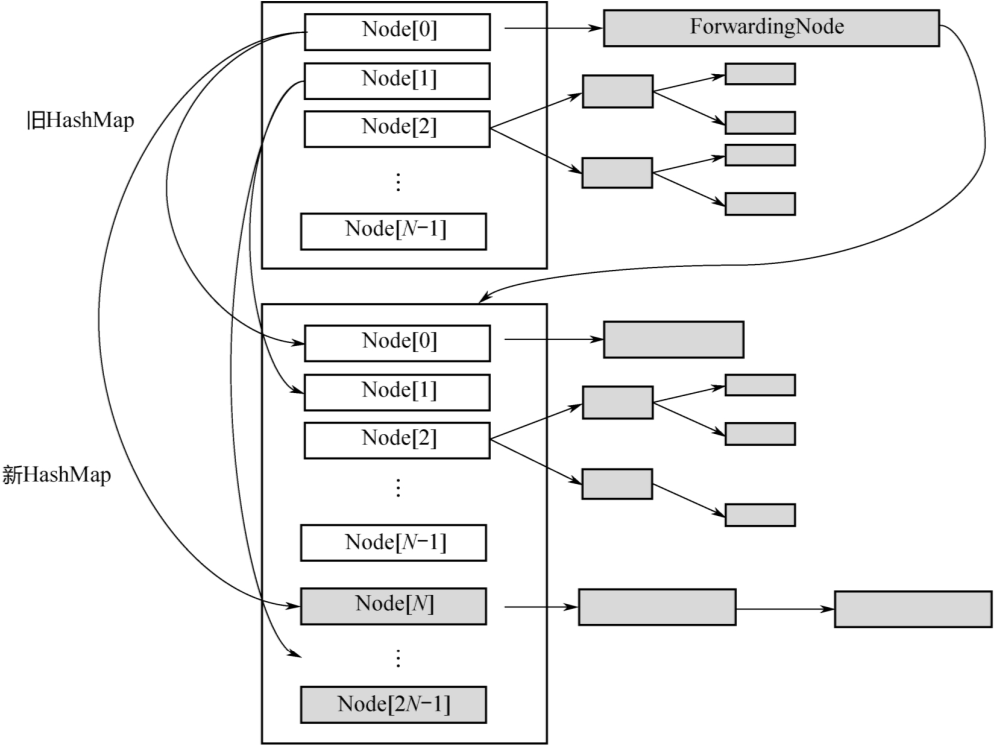
HashMap,其数组长度是旧数组长度的2倍,然后把旧的元素逐个迁移过来。所以,上面的方法参数有2个,第1个参数tab是扩容之前的HashMap,第2个参数nextTab是扩容之后的HashMap。当nextTab=null的时候,方法最初会对nextTab进行初始化。这里有一个关键点要说明:该方法会被多个线程调用,所以每个线程只是扩容旧的HashMap部分,这就涉及如何划分任务的问题。
- 下图为多个线程并行扩容-任务划分示意图。旧数组的长度是N,每个线程扩容一段,一段的长度用变量
stride(步长)来表示,transferIndex表示了整个数组扩容的进度。stride的计算公式如上面的代码所示,即:在单核模式下直接等于n,因为在单核模式下没有办法多个线程并行扩容,只需要1个线程来扩容整个数组;在多核模式下为(n>>>3)/NCPU,并且保证步长的最小值是16。显然,需要的线程个数约为n/stride。transferIndex是ConcurrentHashMap的一个成员变量,记录了扩容的进度。初始值为n,从大到小扩容,每次减stride个位置,最终减至n<=0,表示整个扩容完成。因此,从[0,transferIndex-1]的位置表示还没有分配到线程扩容的部分,从[transfexIndex,n-1]的位置表示已经分配给某个线程进行扩容,当前正在扩容中,或者已经扩容成功。因为transferIndex会被多个线程并发修改,每次减stride,所以需要通过CAS进行操作
- 在扩容未完成之前,有的数组下标对应的槽已经迁移到了新的
HashMap里面,有的还在旧的HashMap里面。这个时候,所有调用get(k,v)的线程还是会访问旧HashMap,怎么处理呢?
下图为扩容过程中的转发示意图:当Node[0]已经迁移成功,而其他Node还在迁移过程中时,如果有线程要读取Node[0]的数据,就会访问失败。为此,新建一个ForwardingNode,即转发节点,在这个节点里面记录的是新的 ConcurrentHashMap的引用。这样,当线程访问到ForwardingNode之后,会去查询新的ConcurrentHashMap。
- 因为数组的长度
tab.length是2的整数次方,每次扩容又是2倍。而Hash函数是hashCode%tab.length,等价于hashCode&(tab.length-1)。这意味着:处于第i个位置的元素,在新的Hash表的数组中一定处于第i个或者第i+n个位置,如下图所示
举个简单的例子:假设数组长度是8,扩容之后是16。
若hashCode=5,5%8=5,扩容后,5%16=5,位置保持不变
若hashCode=24,24%8=0,扩容后,24%16=8,后移8个位置
若hashCode=25,25%8=1,扩容后,25%16=9,后移8个位置
若hashCode=39,39%8=7,扩容后,39%16=7,位置保持不变
...
正因为有这样的规律,所以如下有代码:
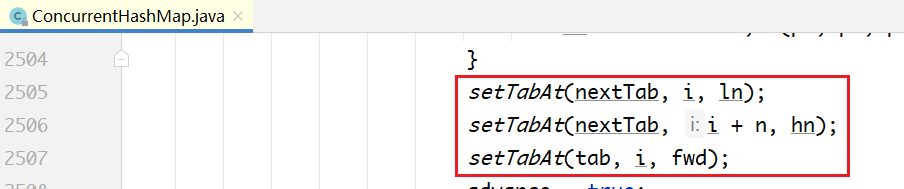
也就是把tab[i]位置的链表或红黑树重新组装成两部分,一部分链接到nextTab[i]的位置,一部分链接到nextTab[i+n]的位置,如上图所示。然后把tab[i]的位置指向一个ForwardingNode节点。
同时,当tab[i]后面是链表时,使用类似于JDK 7中在扩容时的优化方法,从lastRun往后的所有节点,不需依次拷贝,而是直接链接到新的链表头部。从lastRun往前的所有节点,需要依次拷贝。
了解了核心的迁移函数transfer(tab,nextTab),再回头看tryPresize(int size)函数。这个函数的输入是整个Hash表的元素个数,在函数里面,根据需要对整个Hash表进行扩容。想要看明白这个函数,需要透彻地理解sizeCtl变量,下面这段注释摘自源码。
当sizeCtl=-1时,表示整个HashMap正在初始化。
当sizeCtl=某个其他负数时,表示多个线程在对HashMap做并发扩容。
当sizeCtl=cap时,tab=null,表示未初始之前的初始容量(如上面的构造函数所示)。
扩容成功之后,sizeCtl存储的是下一次要扩容的阈值,即上面初始化代码中的n-(n>>>2)=0.75n。
所以,sizeCtl变量在Hash表处于不同状态时,表达不同的含义。明白了这个道理,再来看上面的tryPresize(int size)函数:
/**
* Tries to presize table to accommodate the given number of elements.
*
* @param size number of elements (doesn't need to be perfectly accurate)
*/
private final void tryPresize(int size) {
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY :
tableSizeFor(size + (size >>> 1) + 1);
int sc;
while ((sc = sizeCtl) >= 0) {
Node<K,V>[] tab = table; int n;
if (tab == null || (n = tab.length) == 0) {
n = (sc > c) ? sc : c;
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if (table == tab) {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
table = nt;
sc = n - (n >>> 2);
}
} finally {
sizeCtl = sc;
}
}
}
else if (c <= sc || n >= MAXIMUM_CAPACITY)
break;
else if (tab == table) {
int rs = resizeStamp(n);
if (sc < 0) {
Node<K,V>[] nt;
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
}
}
}tryPresize(int size)是根据期望的元素个数对整个Hash表进行扩容,核心是调用transfer函数。在第一次扩容的时候,sizeCtl会被设置成一个很大的负数U.compareAndSwapInt(this,SIZECTL,sc,(rs << RESIZE_STAMP_SHIFT)+2);之后每一个线程扩容的时候,sizeCtl就加1,U.compareAndSwapInt(this,SIZECTL,sc,sc+1),待扩容完成之后,sizeCtl减1。
ConcurrentSkipListMap/Set
ConcurrentHashMap是一种key无序的HashMap,ConcurrentSkipListMap则是key有序的,实现了NavigableMap接口,此接口又继承了SortedMap接口。
ConcurrentSkipListMap
为什么要使用SkipList实现Map?
在Java的util包中,有一个非线程安全的HashMap,也就是TreeMap,是key有序的,基于红黑树实现。
而在Concurrent包中,提供的key有序的HashMap,也就是ConcurrentSkipListMap,是基于SkipList(跳查表)来实现的。这里为什么不用红黑树,而用跳查表来实现呢?
借用Doug Lea的原话:
The reason is that there are no known efficient lock0free insertion and
deletion algorithms for search trees.也就是目前计算机领域还未找到一种高效的、作用在树上的、无锁的、增加和删除节点的办法。
那为什么SkipList可以无锁地实现节点的增加、删除呢?这要从无锁链表的实现说起。
无锁链表
无锁队列、栈,都是只在队头、队尾进行CAS操作,通常不会有问题。如果在链表的中间进行插入或删除操作,按照通常的CAS做法,就会出现问题!
关于这个问题,Doug Lea的论文中有清晰的论述,此处引用如下:
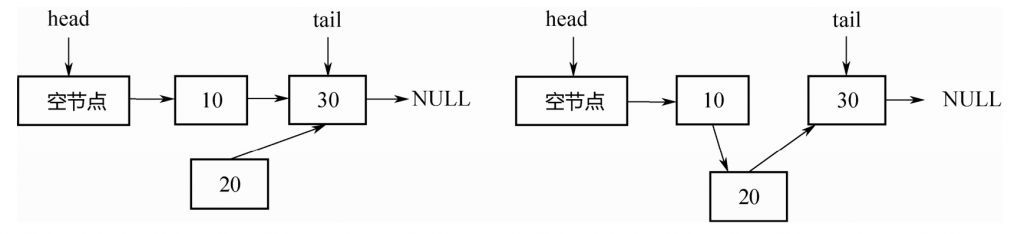
操作1:在节点10后面插入节点20。如下图所示,首先把节点20的next指针指向节点30,然后对节点10的next指针执行CAS操作,使其指向节点20即可。
操作2:删除节点10。如下图所示,只需把头节点的next指针,进行CAS操作到节点30即可。
但是,如果两个线程同时操作,一个删除节点10,一个要在节点10后面插入节点20。并且这两个操作都各自是CAS的,此时就会出现问题。如下图所示,删除节点10,会同时把新插入的节点20也删除掉!这个问题超出了CAS的解决范围。
为什么会出现这个问题呢?
究其原因:在删除节点10的时候,实际受到操作的是节点10的前驱,也就是头节点。节点10本身没有任何变化。故而,再往节点10后插入节点20的线程,并不知道节点10已经被删除了!
针对这个问题,在论文中提出了如下的解决办法,如下图所示,把节点 10 的删除分为两2步:
- 第一步,把节点10的
next指针,mark成删除,即软删除 - 第二步,找机会,物理删除
做标记之后,当线程再往节点10后面插入节点20的时候,便可以先进行判断,节点10是否已经被删除,从而避免在一个删除的节点10后面插入节点20。这个解决方法有一个关键点:“把节点10的next指针指向节点20(插入操作)”和“判断节点10本身是否已经删除(判断操作)”,必须是原子的,必须在1个CAS操作里面完成!
具体的实现有两个办法:
办法一:AtomicMarkableReference
保证每个next是AtomicMarkableReference类型。但这个办法不够高效,Doug Lea 在ConcurrentSkipListMap的实现中用了另一种办法。
办法2:Mark节点
我们的目的是标记节点10已经删除,也就是标记它的next字段。那么可以新造一个Marker节点,使节点10的next指针指向该Marker节点。这样,当向节点10的后面插入节点20的时候,就可以在插入的同时判断节点10的next指针是否指向了一个Marker节点,这两个操作可以在一个CAS操作里面完成。
跳查表
解决了无锁链表的插入或删除问题,也就解决了跳查表的一个关键问题。因为跳查表就是多层链表叠起来的。
下面先看一下跳查表的数据结构(下面所用代码都引用自JDK 7,JDK 8中的代码略有差异,但不影响下面的原理分析)。
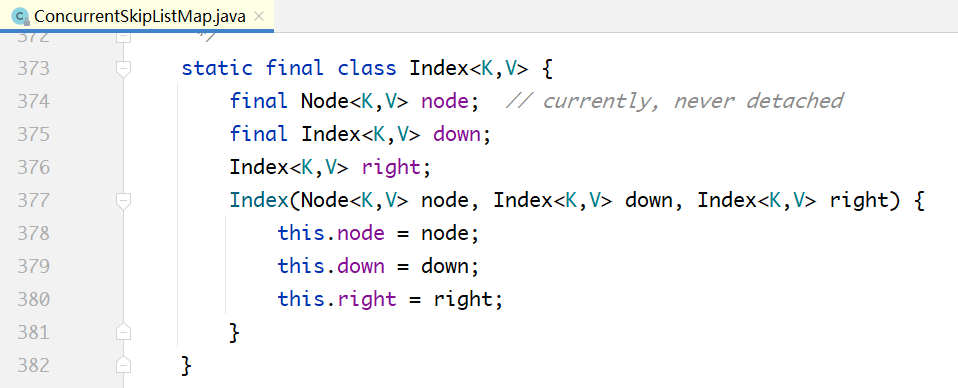
上图中的Node就是跳查表底层节点类型。所有的对都是由这个单向链表串起来的。
上图中的node属性不存储实际数据,指向Node节点。
down属性:每个Index节点,必须有一个指针,指向其下一个Level对应的节点。
right属性:Index也组成单向链表。
整个ConcurrentSkipListMap就只需要记录顶层的head节点即可:
public class ConcurrentSkipListMap<K,V> extends AbstractMap<K,V>
implements ConcurrentNavigableMap<K,V>, Cloneable, Serializable {
// ...
private transient Index<K,V> head;
// ...
}下面详细分析如何从跳查表上查找、插入和删除元素。
put实现分析

/**
* Main insertion method. Adds element if not present, or
* replaces value if present and onlyIfAbsent is false.
* @param key the key
* @param value the value that must be associated with key
* @param onlyIfAbsent if should not insert if already present
* @return the old value, or null if newly inserted
*/
private V doPut(K key, V value, boolean onlyIfAbsent) {
Node<K,V> z; // added node
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
outer: for (;;) {
for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) {
if (n != null) {
Object v; int c;
Node<K,V> f = n.next;
if (n != b.next) // inconsistent read
break;
if ((v = n.value) == null) { // n is deleted
n.helpDelete(b, f);
break;
}
if (b.value == null || v == n) // b is deleted
break;
if ((c = cpr(cmp, key, n.key)) > 0) {
b = n;
n = f;
continue;
}
if (c == 0) {
if (onlyIfAbsent || n.casValue(v, value)) {
@SuppressWarnings("unchecked") V vv = (V)v;
return vv;
}
break; // restart if lost race to replace value
}
// else c < 0; fall through
}
z = new Node<K,V>(key, value, n);
if (!b.casNext(n, z))
break; // restart if lost race to append to b
break outer;
}
}
int rnd = ThreadLocalRandom.nextSecondarySeed();
if ((rnd & 0x80000001) == 0) { // test highest and lowest bits
int level = 1, max;
while (((rnd >>>= 1) & 1) != 0)
++level;
Index<K,V> idx = null;
HeadIndex<K,V> h = head;
if (level <= (max = h.level)) {
for (int i = 1; i <= level; ++i)
idx = new Index<K,V>(z, idx, null);
}
else { // try to grow by one level
level = max + 1; // hold in array and later pick the one to use
@SuppressWarnings("unchecked")Index<K,V>[] idxs =
(Index<K,V>[])new Index<?,?>[level+1];
for (int i = 1; i <= level; ++i)
idxs[i] = idx = new Index<K,V>(z, idx, null);
for (;;) {
h = head;
int oldLevel = h.level;
if (level <= oldLevel) // lost race to add level
break;
HeadIndex<K,V> newh = h;
Node<K,V> oldbase = h.node;
for (int j = oldLevel+1; j <= level; ++j)
newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);
if (casHead(h, newh)) {
h = newh;
idx = idxs[level = oldLevel];
break;
}
}
}
// find insertion points and splice in
splice: for (int insertionLevel = level;;) {
int j = h.level;
for (Index<K,V> q = h, r = q.right, t = idx;;) {
if (q == null || t == null)
break splice;
if (r != null) {
Node<K,V> n = r.node;
// compare before deletion check avoids needing recheck
int c = cpr(cmp, key, n.key);
if (n.value == null) {
if (!q.unlink(r))
break;
r = q.right;
continue;
}
if (c > 0) {
q = r;
r = r.right;
continue;
}
}
if (j == insertionLevel) {
if (!q.link(r, t))
break; // restart
if (t.node.value == null) {
findNode(key);
break splice;
}
if (--insertionLevel == 0)
break splice;
}
if (--j >= insertionLevel && j < level)
t = t.down;
q = q.down;
r = q.right;
}
}
}
return null;
}在底层,节点按照从小到大的顺序排列,上面的index层间隔地串在一起,因为从小到大排列。查找的时候,从顶层index开始,自左往右、自上往下,形成图示的遍历曲线。假设要查找的元素是32,遍历过程如下:
- 先遍历第2层
Index,发现在21的后面 - 从21下降到第1层
Index,从21往后遍历,发现在21和35之间 - 从21下降到底层,从21往后遍历,最终发现在29和35之间
在整个的查找过程中,范围不断缩小,最终定位到底层的两个元素之间。
关于上面的put(…)方法,有一个关键点需要说明:在通过findPredecessor找到了待插入的元素在[b,n]之间之后,并不能马上插入。因为其他线程也在操作这个链表,b、n都有可能被删除,所以在插入之前执行了一系列的检查逻辑,而这也正是无锁链表的复杂之处。
remove(…)分析
// 若找到了(key, value)就删除,并返回value;找不到就返回null
final V doRemove(Object key, Object value) {
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
V result = null;
Node<K,V> b;
outer: while ((b = findPredecessor(key, cmp)) != null &&
result == null) {
for (;;) {
Node<K,V> n; K k; V v; int c;
if ((n = b.next) == null)
break outer;
else if ((k = n.key) == null)
break;
else if ((v = n.val) == null)
unlinkNode(b, n);
else if ((c = cpr(cmp, key, k)) > 0)
b = n;
else if (c < 0)
break outer;
else if (value != null && !value.equals(v))
break outer;
else if (VAL.compareAndSet(n, v, null)) {
result = v;
unlinkNode(b, n);
break; // loop to clean up
}
}
}
if (result != null) {
tryReduceLevel();
addCount(-1L);
}
return result;
}上面的删除方法和插入方法的逻辑非常类似,因为无论是插入,还是删除,都要先找到元素的前驱,也就是定位到元素所在的区间[b,n]。在定位之后,执行下面几个步骤:
- 如果发现
b、n已经被删除了,则执行对应的删除清理逻辑 - 否则,如果没有找到待删除的
(k, v),返回null - 如果找到了待删除的元素,也就是节点
n,则把n的value置为null,同时在n的后面加上Marker节点,同时检查是否需要降低Index的层次
get分析
private V doGet(Object key) {
Index<K,V> q;
VarHandle.acquireFence();
if (key == null)
throw new NullPointerException();
Comparator<? super K> cmp = comparator;
V result = null;
if ((q = head) != null) {
outer: for (Index<K,V> r, d;;) {
while ((r = q.right) != null) {
Node<K,V> p; K k; V v; int c;
if ((p = r.node) == null || (k = p.key) == null ||
(v = p.val) == null)
RIGHT.compareAndSet(q, r, r.right);
else if ((c = cpr(cmp, key, k)) > 0)
q = r;
else if (c == 0) {
result = v;
break outer;
}
else
break;
}
if ((d = q.down) != null)
q = d;
else {
Node<K,V> b, n;
if ((b = q.node) != null) {
while ((n = b.next) != null) {
V v; int c;
K k = n.key;
if ((v = n.val) == null || k == null ||
(c = cpr(cmp, key, k)) > 0)
b = n;
else {
if (c == 0)
result = v;
break;
}
}
}
break;
}
}
}
return result;
}无论是插入、删除,还是查找,都有相似的逻辑,都需要先定位到元素位置[b,n],然后判断b、n是否已经被删除,如果是,则需要执行相应的删除清理逻辑。这也正是无锁链表复杂的地方。
ConcurrentSkipListSet
如下面代码所示,ConcurrentSkipListSet只是对ConcurrentSkipListMap的简单封装,此处不再进一步展开叙述。
public class ConcurrentSkipListSet<E>
extends AbstractSet<E>
implements NavigableSet<E>, Cloneable, java.io.Serializable {
// 封装了一个ConcurrentSkipListMap
private final ConcurrentNavigableMap<E,Object> m;
public ConcurrentSkipListSet() {
m = new ConcurrentSkipListMap<E,Object>();
}
public boolean add(E e) {
return m.putIfAbsent(e, Boolean.TRUE) == null;
}
// ...
}以上就是本文的全部内容。欢迎小伙伴们积极留言交流~~~




















文章评论