数据结构的概念

什么是数据结构

数据结构(data structure)是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。

一句话解释：存数据的，而且是在内存中存！

常见的数据结构

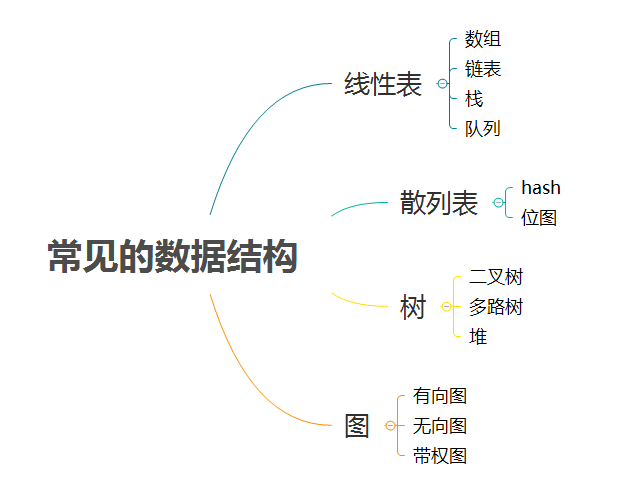
算法的概念

什么是算法

算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。

一句话描述：算法是一种解决特定问题的思路。

比如：LRU算法，最近最少使用，解决的就是当空间不够用时，应该淘汰谁的问题，这是一种策略，不是唯一的答案，所以算法无对错，只有好和不好。

常见算法

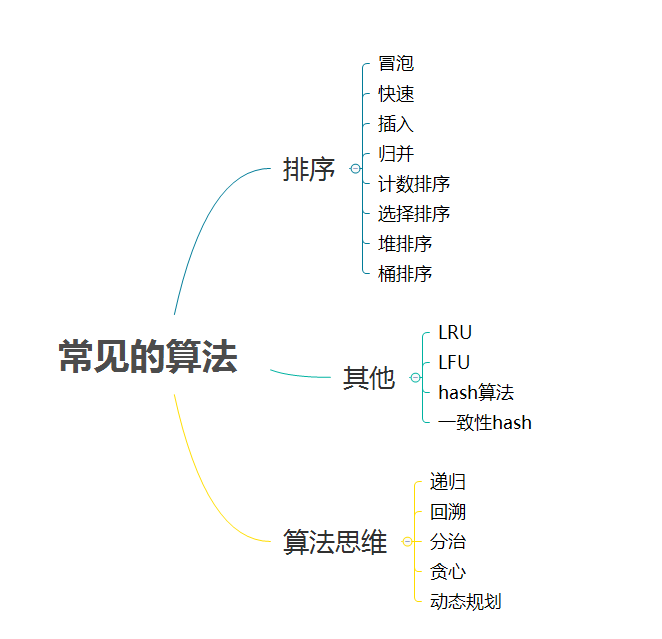
算法复杂度

数据结构和算法本质上是”快“和"省"，所以代码的执行效率是非常重要的度量，我们采用时间复杂度和空间复杂度来计算。

时间复杂度

大O复杂度表示法

int sum(int n){
    int s=0; //t
    int i=1; //t
    for(;i<=n;i++){ //t*n
       s=s+i;    //t*n 
    }
    return s;    //t
}
n=100
1+1+100n+100n+1=200n+3

我们假设执行一行代码的时间为t，通过估算，代码的执行时间T(n)与执行次数成正比，记做：

T(n)=O(f(n))

T(n)：代码执行时间
n：数据规模
f(n)：每行代码执行次数总和
O：代码的执行时间与f(n)表达式成正比

上面的例子中的T(n)=O(2n+2)，当n无限大时，低阶、常量、系统都可以忽略，所以T(n)=O(n)，即上例中的时间复杂度为O(n)，也就是代码执行时间随着数据规模的增加而增长。

int sum(int n){
    int s=0;
    int i=1;
    int j=1;
    for(;i<=n;i++){// n
      j=1;
      for(;j<=n;j++){ //n*n
         s=s+i+j;   //n*n
      } 
    }
    return s;
}

上例中T(n)=O(n*n)，也就是代码执行时间随着数据规模的增加而平方增长。

即：上例中的时间复杂度为O(n^2)。

时间复杂度也成为渐进时间复杂度。

计算时间复杂度的技巧

计算循环执行次数最多的代码
总复杂度=量级最大的复杂度

比如把上面两段代码合在一起：

int sum(int n){
int sum(int n){
    int s=0;
    int i=1;
    int j=1;
    for(;i<=n;i++){ //t*n
        s=s+i;    //t*n 
    }
    for(;i<=n;i++){// n
        j=1;
        for(;j<=m;j++){ //n*m
            s=s+i+j;   //n*m
        }
    }
    return s;
}

时间复杂度为O(n^2) ，即嵌套代码的复杂度等于嵌套内外代码复杂度的乘积(乘法法则)。

常见的时间复杂度

O(1)

这种是最简单的，也是最好理解的，就是常量级

不是只执行了一行代码，只要代码的执行不随着数据规模(n)的增加而增加，就是常量级

在实际应用中，通常使用冗余字段存储来将O(n)变成O(1)，比如Redis中有很多这样的操作用来提升访问性能

比如:SDS、字典、跳跃表等

O(logn)、O(nlogn)

i = 1;
while(i <= n){
  i = i * 2;// 执行最多
}

2^x=n

x=log2n

忽略系数为logn

T(n)=O(logn）

如果将该代码执行n遍

则时间复杂度记录为:T(n)=O(n*logn），即O(nlogn)

快速排序、归并排序的时间复杂度都是O(nlogn)

O(n)

这个前面已经讲了，很多线性表的操作都是O(n),这也是最常见的一个时间复杂度

比如：数组的插入删除、链表的遍历等

O(m+n)

代码的时间复杂度由两个数据的规模来决定：

 int sum(int m,int n){
    int s1=0;
    int s2=0;
    int i=1;
    int j=1;
    for(;i<=m;i++){
      s1=s1+i; // 执行最多
    }
    for(;j<=n;j++){
      s2=s2+j; //执行最多
    }
    return s1+s2;
 }

m和n是代码的两个数据规模，而且不能确定谁更大，此时代码的复杂度为两段时间复杂度之和，即：T(n)=O(m+n)，记作：O(m+n)

O(m*n)

int sum(int m,int n){
    int s=0;
    int i=1;
    int j=1;
    for(;i<=m;i++){// m
      j=1;
      for(;j<=n;j++){ //m*n
        s=s+i+j;   //m*n
       }
     }
    return s;
}

根据乘法法则代码的复杂度为两段时间复杂度之积，即：

T(n)=O(mn)，记作：O(mn)

当m==n时，为O(n^2)