概念
散列表也叫作哈希表(hash table),这种数据结构提供了键(Key)和值(Value)的映射关系。只要给出一个Key,就可以高效查找到它所匹配的Value,时间复杂度接近于O(1)。
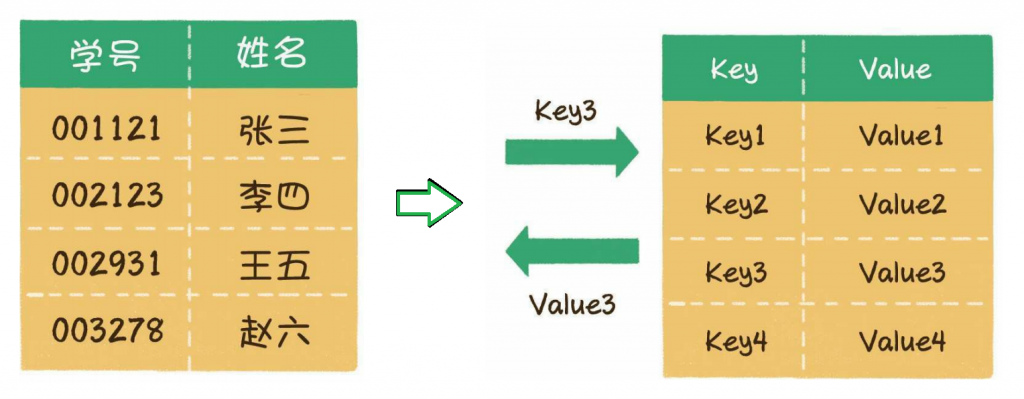
存储原理
哈希函数
散列表在本质上也是一个数组,散列表的Key则是以字符串类型为主的,通过hash函数把Key和数组下标进行转换。作用是把任意长度的输入通过散列算法转换成固定类型、固定长度的散列值。
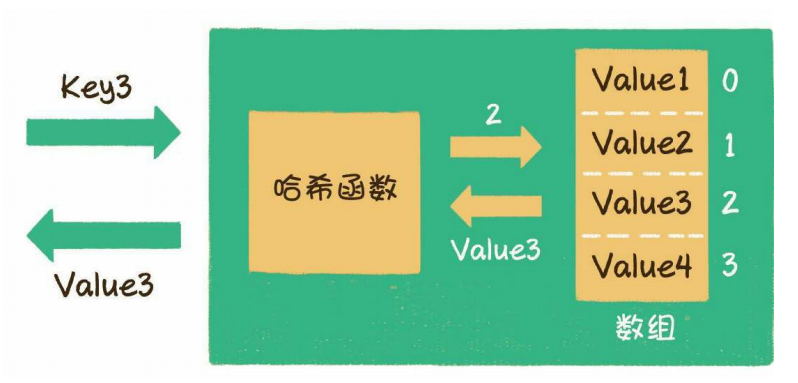
以Java为例:
//数组下标=取key的hashcode模数组的长度后的余数
index = HashCode (Key) % Array.length
int index=Math.abs("Hello".hashCode())%10; (0-9)这是最简单的计算方式
还有很多hash函数:CRC16、CRC32、siphash 、murmurHash、times 33等
此种Hash计算方式为固定Hash方式,也称为传统Hash
该方式在数组固定时,可以快速检索
但当数组长度变化时,需要重新计算数组下标,此时根据key检索将出现问题
所以说传统Hash法虽然比较简单,但不利于扩展,如果要扩展可以采用一致性Hash法
操作
- 写操作(put)
写操作就是在散列表中插入新的键值对(在JDK中叫作Entry或Node)
第1步,通过哈希函数,把Key转化成数组下标
第2步,如果数组下标对应的位置没有元素,就把这个Entry填充到数组下标的位置

- Hash冲突(碰撞)
由于数组的长度是有限的,当插入的Entry越来越多时,不同的Key通过哈希函数获得的下标有可能是相同的,这种情况,就叫作哈希冲突:
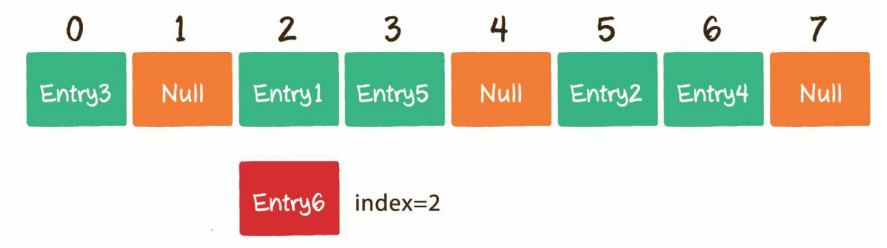
解决哈希冲突的方法主要有两种:
开放寻址法
开放寻址法的原理是当一个Key通过哈希函数获得对应的数组下标已被占用时,就寻找下一个空档位置:

在Java中,ThreadLocal所使用的就是开放寻址法
链表法
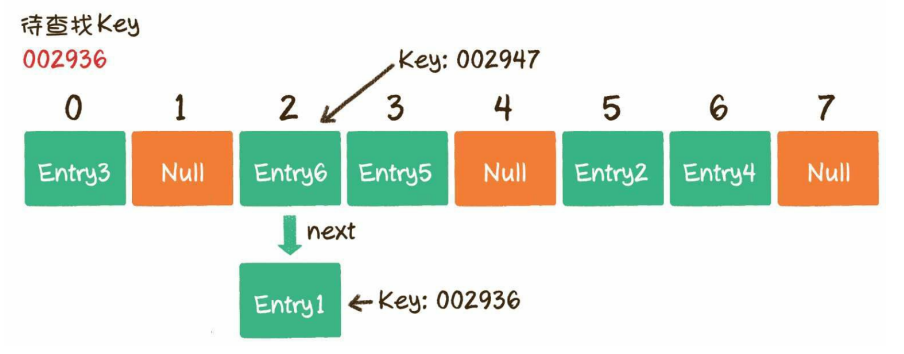
数组的每一个元素不仅是一个Entry对象,还是一个链表的头节点。每一个Entry对象通过next指针指向它的下一个Entry节点。当新来的Entry映射到与之冲突的数组位置时,只需要插入到对应的链表中即可,默认next指向null:

在Entry中保存key和值,以及next指针:
Entry{
int key;
Object value;
Entry next;
}当根据key查找值的时候,在index=2的位置是一个单链表
遍历该单链表,再根据key即可取值
- 读操作(get)
读操作就是通过给定的Key,在散列表中查找对应的Value
第1步,通过哈希函数,把Key转化成数组下标
第2步,找到数组下标所对应的元素,如果key不正确,说明产生了hash冲突,则顺着头节点遍历该单链表,再根据key即可取值
- Hash扩容(resize)
散列表是基于数组实现的,所以散列表需要扩容
当经过多次元素插入,散列表达到一定饱和度时,Key映射位置发生冲突的概率会逐渐提高。这样一来,大量元素拥挤在相同的数组下标位置,形成很长的链表,对后续插入操作和查询操作的性能都有很大影响
影响扩容的因素有两个:
- Capacity:HashMap的当前长度
- LoadFactor:HashMap的负载因子(阈值),默认值为0.75f
当HashMap.Size >= Capacity×LoadFactor时,需要进行扩容
扩容的步骤:
- 扩容,创建一个新的Entry空数组,长度是原数组的2倍
- 重新Hash,遍历原Entry数组,把所有的Entry重新Hash到新数组中

关于HashMap的实现,JDK 8和以前的版本有着很大的不同。当多个Entry被Hash到同一个数组下标位置时,为了提升插入和查找的效率,HashMap会把Entry的链表转化为红黑树这种数据结构。
JDK1.8前在HashMap扩容时,会反序单链表,这样在高并发时会有死循环的可能。
实现代码:
package com.rubin.datastructure.map;
public class RubinHashMap {
private Node[] nodes;
private int size;
private int cap;
private float loadFactor;
public RubinHashMap(int cap) {
nodes = new Node[cap];
this.cap = cap;
loadFactor = 0.75f;
}
static class Node {
String key;
String value;
Node next;
public Node(String key, String value) {
this.key = key;
this.value = value;
}
}
public void put(String key, String value) {
int index = doHash(key);
Node head = nodes[index];
if (head == null) {
nodes[index] = new Node(key, value);
} else {
Node tmp = head;
while (true) {
if (tmp.key.equals(key)) {
tmp.value = value;
break;
}
if (tmp.next == null) {
tmp.next = new Node(key, value);
break;
}
tmp = tmp.next;
}
}
++size;
if (size >= (cap * loadFactor)) {
resize();
}
}
public String get(String key) {
if (size == 0) {
return null;
}
int index = doHash(key);
Node tmp = nodes[index];
while (tmp != null) {
if (tmp.key.equals(key)) {
return tmp.value;
}
tmp = tmp.next;
}
return null;
}
private void resize() {
cap = cap << 1;
size = 0;
Node[] newNodes = new Node[cap];
for (int i = 0; i < nodes.length; i++) {
Node head = nodes[i];
if (head == null) {
continue;
}
rehash(head, newNodes);
}
nodes = newNodes;
}
private void rehash(Node head, Node[] newNodes) {
Node tmp = head, next = head.next;
while (true) {
int index = doHash(tmp.key);
Node h = newNodes[index];
if (h == null) {
newNodes[index] = tmp;
} else {
Node tail = findTail(h);
tail.next = tmp;
}
tmp.next = null;
tmp = next;
if (tmp == null) {
break;
}
next = tmp.next;
}
}
private int doHash(String key) {
return Math.abs(key.hashCode() % cap);
}
private Node findTail(Node head) {
if (head == null) {
throw new RuntimeException("the head is null");
}
Node tail = head;
while (tail.next != null) {
tail = tail.next;
}
return tail;
}
public static void main(String[] args) {
RubinHashMap rubinHashMap = new RubinHashMap(2);
for (int i = 0; i < 10; i++) {
rubinHashMap.put("key" + i, "value" + i);
}
System.out.println(rubinHashMap.get("key5"));
System.out.println(rubinHashMap.get("key10"));
System.out.println(rubinHashMap.get("key3"));
}
}
时间复杂度
写操作: O(1) + O(m) = O(m) (m为单链元素个数)
读操作:O(1) + O(m) (m为单链元素个数)
Hash冲突写单链表:O(m)
Hash扩容:O(n) (n是数组元素个数)
Hash冲突读单链表:O(m) (m为单链元素个数)
优缺点
优点:读写快
缺点:哈希表中的元素是没有被排序的、Hash冲突、扩容 重新计算
应用
HashMap
JDK1.7中HashMap使用一个table数组来存储数据,用key的hashcode取模来决定key会被放到数组里的位置,如果hashcode相同,或者hashcode取模后的结果相同,那么这些key会被定位到Entry数组的同一个格子里,这些key会形成一个链表,在极端情况下比如说所有key的hashcode都相同,将会导致这个链表会很长,那么put/get操作需要遍历整个链表,那么最差情况下时间复杂度变为O(n)。
扩容死链:
针对JDK1.7中的这个性能缺陷,JDK1.8中的table数组中可能存放的是链表结构,也可能存放的是红黑树结构,如果链表中节点数量不超过8个则使用链表存储,超过8个会调用treeifyBin函数,将链表转换为红黑树。那么即使所有key的hashcode完全相同,由于红黑树的特点,查找某个特定元素,也只需要O(logn)的开销。

字典
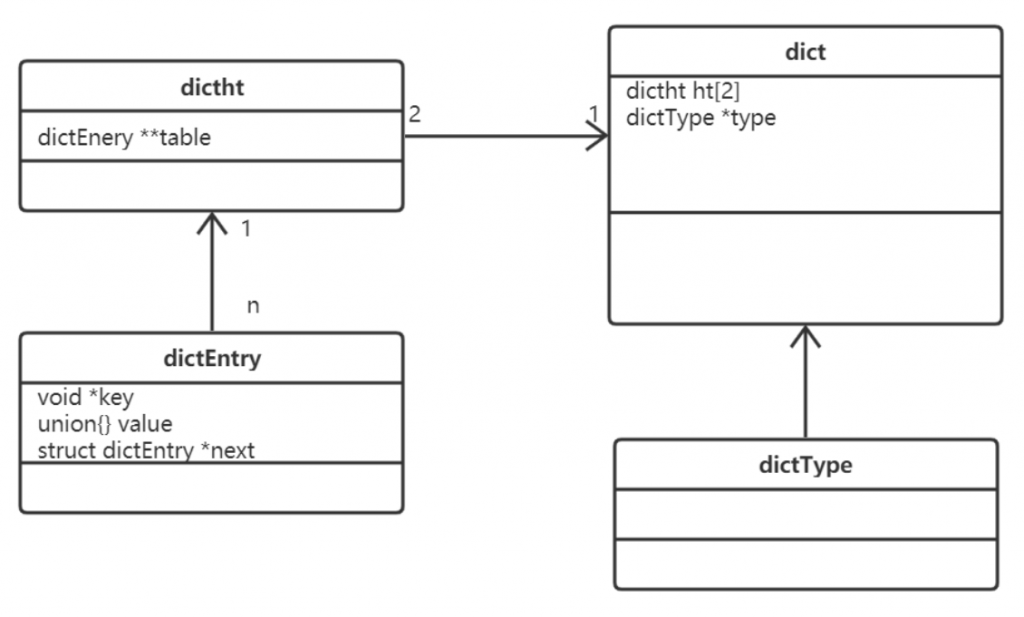
Redis字典dict又称散列表(hash),是用来存储键值对的一种数据结构
Redis整个数据库是用字典来存储的
对Redis进行CURD操作其实就是对字典中的数据进行CURD操作
Redis字典实现包括:字典(dict)、Hash表(dictht)、Hash表节点(dictEntry)
布隆过滤器
布隆过滤器(Bloom Filter)是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机hash映射函数。
布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法。
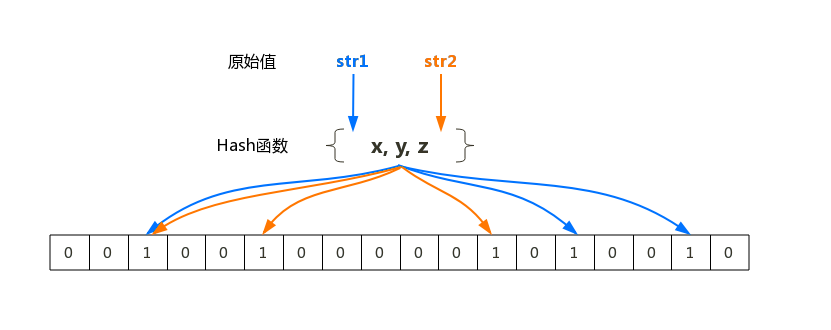
布隆过滤器的原理是,当一个元素被加入集合时,通过K个Hash函数将这个元素映射成一个数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。
位图
试想以下,如果有一个很大的 int 数组,如 10000000,数组中每一个数值都要占用 4 个字节,则一共需要占用 10000000 * 4 = 40000000 个字节,即 40000000 / 1024.0 / 1024.0 = 38 M。
如果使用 bit 来存放上述 10000000 个元素,只需要 10000000 个 bit 即可, 10000000 / 8.0 / 1024.0 / 1024.0 = 1.19 M 左右,可以看到 bitmap 可以大大的节约内存。
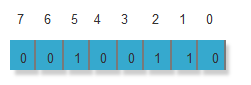
使用 bit 来表示数组 [1, 2, 5] 如下所示,可以看到只用 1 字节即可表示:
以上就是本文的全部内容。欢迎各位小伙伴们积极留言交流~~~
文章评论