线性表（Linear List）就是数据排成像一条线一样的结构，数据只有前后两个方向：

数组

概念

数组（Array）是有限个相同类型的变量所组成的有序集合，数组中的每一个变量被称为元素。数组是最为简单、最为常用的数据结构。

数组下标从零开始，为什么呢？

存储原理

数组用一组连续的内存空间来存储一组具有相同类型的数据：

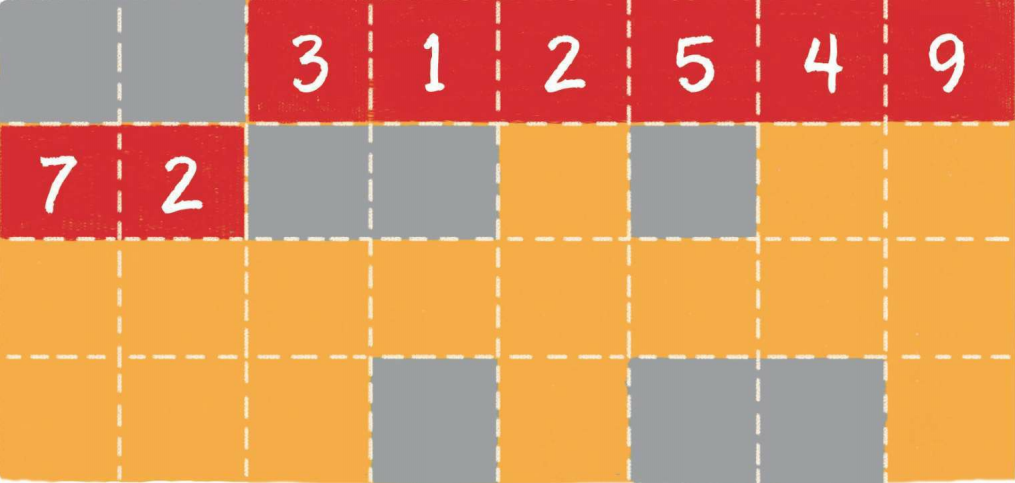
模拟内存存储：

• 灰色格子：被使用的内存
• 橙色格子：空闲的内存
• 红色格子：数组占用的内存

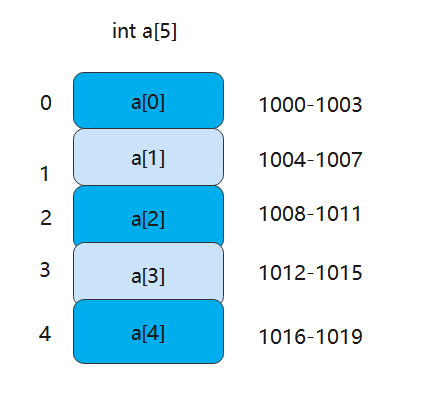
数组可以根据下标随机访问数据。比如一个整型数据 int[] 长度为5：

假设首地址是：1000，int是4字节（32位）,实际内存存储是位，随机元素寻址：

a[i]_address=a[0]_address+i*4

该公式解释了三个方面：

• 连续性分配
• 相同的类型
• 下标从0开始

操作

• 读取元素

根据下标读取元素的方式叫作随机读取：

int n=nums[2]

• 更新元素

nums[3]= 10;

注意不要数组越界

读取和更新都可以随机访问，时间复杂度为O(1)

• 插入元素

有三种情况：

尾部插入

在数据的实际元素数量小于数组长度的情况下：

直接把插入的元素放在数组尾部的空闲位置即可，等同于更新元素的操作：

a[6]=10

中间插入

在数据的实际元素数量小于数组长度的情况下：

由于数组的每一个元素都有其固定下标，所以首先把插入位置及后面的元素向后移动，腾出地方，再把要插入的元素放到对应的数组位置上：

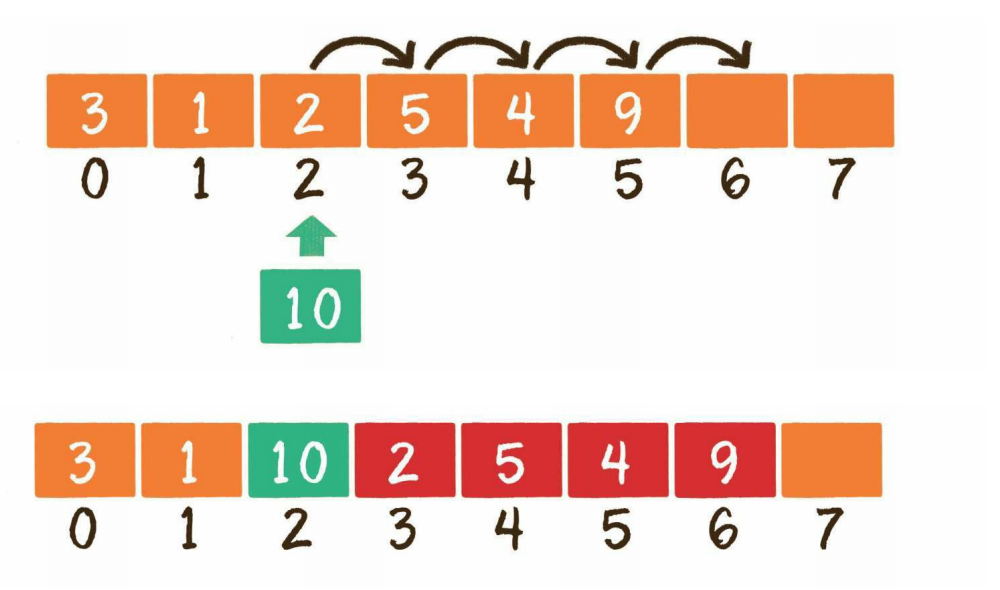
超范围插入

假如现在有一个数组，已经装满了元素，这时还想插入一个新元素，或者插入位置是越界的，这时就要对原数组进行扩容：可以创建一个新数组，长度是旧数组的2倍，再把旧数组中的元素统统复制过去，这样就实现了数组的扩容：

int[] numsNew=new int[nums.length*2];
System.arraycopy(nums,0,numsNew,0,nums.length);
// 原数组就丢掉了，资源浪费
nums=numsNew;

• 删除元素

数组的删除操作和插入操作的过程相反，如果删除的元素位于数组中间，其后的元素都需要向前挪动1位：

for(int i=p;i<nums.length;i++){
  nums[i-1]=nums[i];
}

完整的代码：

package com.rubin.datastructure.array;

import java.util.Arrays;

public class RubinIntArray {

    private int[] items;

    private int size;

    public RubinIntArray() {
        this.items = new int[10];
        this.size = 0;
    }

    public int add(int item) {
        if (size == items.length) {
            resize();
        }
        int index = size;
        items[index] = item;
        ++size;
        return index;
    }

    public int insert(int index, int item) {
        if (index > size) {
            throw new RuntimeException("the index is out of bound");
        }
        if (index == size) {
            add(item);
            return 0;
        }
        if (size == items.length) {
            resize();
        }
        for (int i = size; i > index; i--) {
            items[i] = items[i - 1];
        }
        int oldValue = items[index];
        items[index] = item;
        ++size;
        return oldValue;
    }

    public int update(int index, int item) {
        if (index > size) {
            throw new RuntimeException("the index is out of bound");
        }
        int oldValue = items[index];
        items[index] = item;
        return oldValue;
    }

    public int get(int index) {
        if (index > size) {
            throw new RuntimeException("the index is out of bound");
        }
        return items[index];
    }

    public int delete(int index) {
        if (index >= size) {
            throw new RuntimeException("the index is out of bound");
        }
        int oldValue = items[index];
        if (index == (size -1)) {
            items[index] = 0;
            --size;
            return oldValue;
        }
        for (int i = index + 1; i < size; i++) {
            items[i - 1] = items[i];
        }
        --size;
        items[size] = 0;
        return oldValue;
    }

    public int size() {
        return size;
    }

    private void resize() {
        int[] newItems = new int[items.length * 2];
        System.arraycopy(items, 0, newItems, 0, items.length);
        items = newItems;
    }

    @Override
    public String toString() {
        return Arrays.toString(items);
    }

}

package com.rubin.datastructure.array;

public class Main {

    public static void main(String[] args) {
        RubinIntArray rubinIntArray = new RubinIntArray();
        System.out.println(rubinIntArray);
        for (int i = 0; i < 19; i++) {
            rubinIntArray.add(i);
        }
        System.out.println(rubinIntArray);
        rubinIntArray.insert(19, 19);
        System.out.println(rubinIntArray);
        rubinIntArray.insert(0, 20);
        System.out.println(rubinIntArray);
        rubinIntArray.update(0, 100);
        System.out.println(rubinIntArray);
        rubinIntArray.delete(rubinIntArray.size() - 1);
        System.out.println(rubinIntArray);
        rubinIntArray.delete(0);
        System.out.println(rubinIntArray);
    }

}

时间复杂度

读取和更新都是随机访问，所以是O(1)。

插入数组扩容的时间复杂度是O(n)，插入并移动元素的时间复杂度也是O(n)，综合起来插入操作的时间复杂度是O(n)。

删除操作，只涉及元素的移动，时间复杂度也是O(n)。

优缺点

优点：数组拥有非常高效的随机访问能力，只要给出下标，就可以用常量时间找到对应元素。

缺点：插入和删除元素方面。由于数组元素连续紧密地存储在内存中，插入、删除元素都会导致大量元素被迫移动，影响效率 (ArrayList LinkedList )。

申请的空间必须是连续的，也就是说即使有空间也可能因为没有足够的连续空间而创建失败。如果超出范围，需要重新申请内存进行存储，原空间就浪费了。

应用

数组是基础的数据结构，应用太广泛了，ArrayList、Redis、消息队列等等。

数据结构和算法的可视化网站：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html。

链表

概念

链表（linked list）是一种在物理上非连续、非顺序的数据结构，由若干节点（node）所组成。

链表中数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。

常见的链表包括：单链表、双向链表、循环链表。

• 单链表

单向链表的每一个节点又包含两部分，一部分是存放数据的变量data，另一部分是指向下一个节点的指针next：

Node{
  int data;
  Node next;  
}

• 双向链表

双向链表的每一个节点除了拥有data和next指针，还拥有指向前置节点的prev指针：

Node{
  int data;
  Node next;  
  Node prev;
}

• 循环链表

链表的尾节点指向头节点形成一个环，称为循环链表：

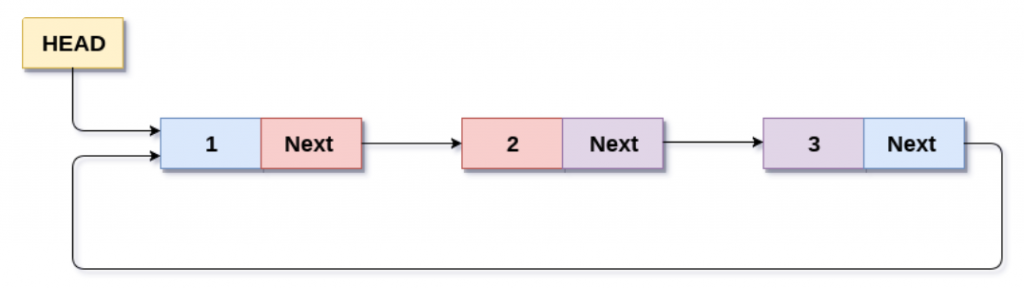
存储原理

数组在内存中的存储方式是顺序存储（连续存储），链表在内存中的存储方式则是随机存储（链式存储）。

链表的每一个节点分布在内存的不同位置，依靠next指针关联起来。这样可以灵活有效地利用零散的碎片空间。

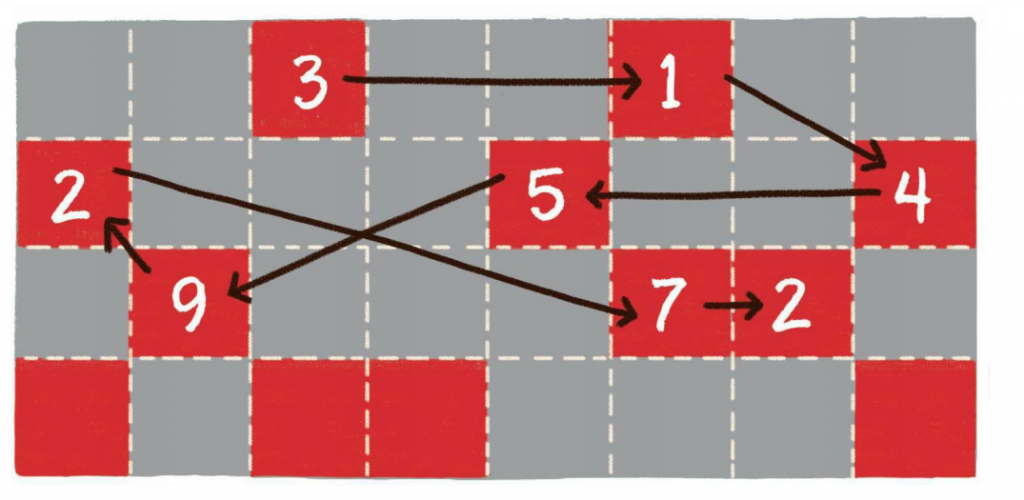
链表的第1个节点被称为头节点（3），没有任何节点的next指针指向它，或者说它的前置节点为空。头节点用来记录链表的基地址，有了它，我们就可以遍历得到整条链表。链表的最后1个节点被称为尾节点（2），它指向的next为空。

操作

• 查找节点

在查找元素时，链表只能从头节点开始向后一个一个节点逐一查找：

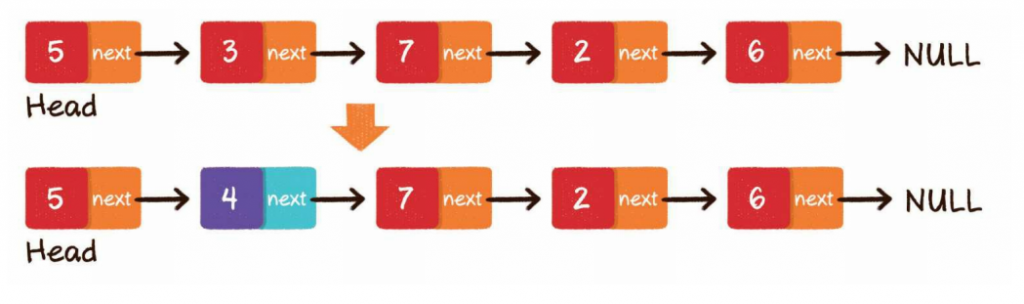
• 更新节点

找到要更新的节点，然后把旧数据替换成新数据：

• 插入节点

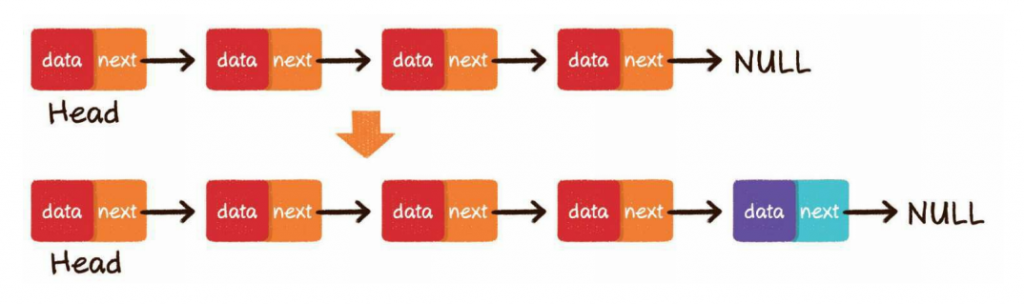
尾部插入

把最后一个节点的next指针指向新插入的节点即可：

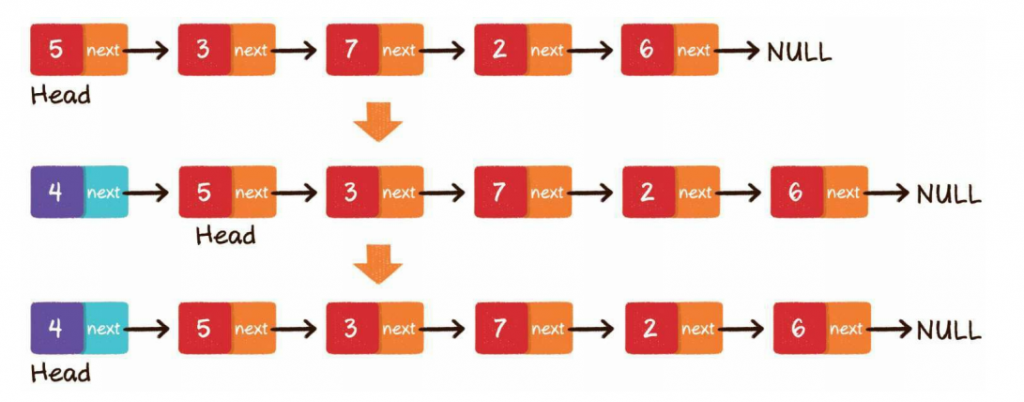
头部插入

第1步，把新节点的next指针指向原先的头节点

第2步，把新节点变为链表的头节点

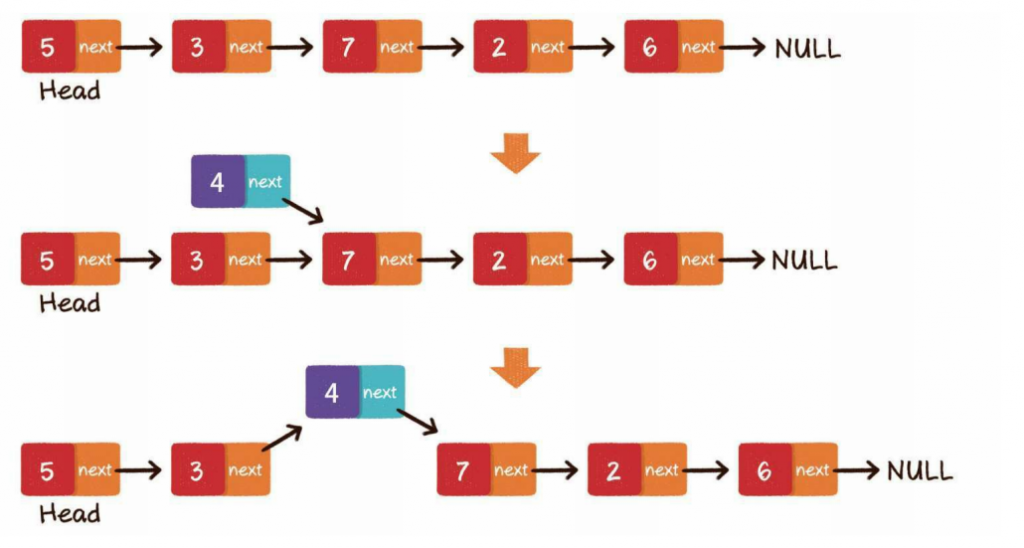
中间插入

第1步，新节点的next指针，指向插入位置的节点

第2步，插入位置前置节点的next指针，指向新节点

只要内存空间允许，能够插入链表的元素是无限的，不需要像数组那样考虑扩容的问题。

• 删除节点

尾部删除

把倒数第2个节点的next指针指向空即可：

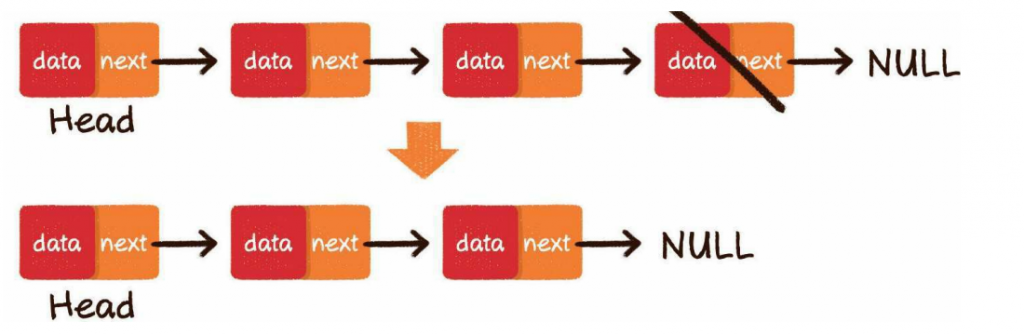
头部删除

把链表的头节点设为原先头节点的next指针即可：

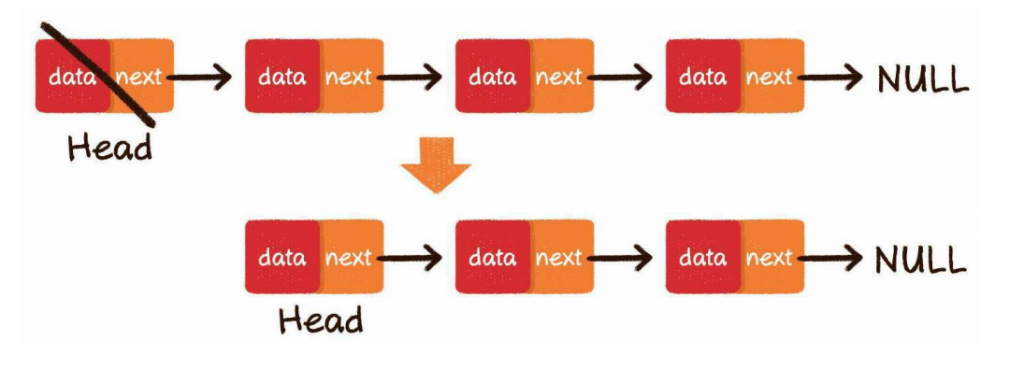
中间删除

把要删除节点的前置节点的next指针，指向要删除元素的下一个节点即可：

完整代码：

package com.rubin.datastructure.linkedlist;

import lombok.Data;

@Data
public class RubinNode {

    private int id;

    private String name;

    private RubinNode next;

    public RubinNode() {
    }

    public RubinNode(int id, String name) {
        this.id = id;
        this.name = name;
    }

    @Override
    public String toString() {
        return "RubinNode{" +
                "id=" + id +
                ", name='" + name + '\'' +
                '}';
    }

}

package com.rubin.datastructure.linkedlist;

public class RubinLinkedList {

    private RubinNode head;

    public RubinLinkedList() {
        this.head = new RubinNode(0, "");
    }

    /**
     * 添加节点：从头插入
     *
     * @param node  
     */
    public void addNode(RubinNode node) {
        //从头插入
        RubinNode tmp = head;
        while (true) {
            //到尾节点
            if (tmp.getNext() == null) {
                break;
            }
            //后移一个节点
            tmp = tmp.getNext();
        }
        tmp.setNext(node);
    }

    public void addByIdOrder(RubinNode node) {
        //从头插入
        RubinNode tmp = head;
        while (true) {
            //到尾节点
            if (tmp.getNext() == null) {
                break;
            }
            //节点存在
            if (tmp.getNext().getId() == node.getId()) {
                break;
            }
            if (tmp.getNext().getId() > node.getId()) {
                break;
            }
            tmp = tmp.getNext();
        }
        //交换位置
        node.setNext(tmp.getNext());
        tmp.setNext(node);
    }

    public void showList() {
        if (head.getNext() == null) {
            System.out.println("the list is empty");
            return;
        }
        RubinNode tmp = head.getNext();
        while (tmp != null) {
            System.out.println(tmp);
            tmp = tmp.getNext();
        }

    }

}

package com.rubin.datastructure.linkedlist;

public class Main {

    public static void main(String[] args) {
        RubinNode n1 = new RubinNode(1, "张飞");
        RubinNode n2 = new RubinNode(2, "关羽");
        RubinNode n3 = new RubinNode(3, "赵云");
        RubinNode n4 = new RubinNode(4, "黄忠");
        RubinNode n5 = new RubinNode(5, "马超");
        RubinLinkedList rubinLinkedList = new RubinLinkedList();
        rubinLinkedList.addByIdOrder(n4);
        rubinLinkedList.addByIdOrder(n5);
        rubinLinkedList.addByIdOrder(n1);
        rubinLinkedList.addByIdOrder(n2);
        rubinLinkedList.addByIdOrder(n3);
        rubinLinkedList.showList();
    }

}

时间复杂度

查找节点 ： O(n)

插入节点：O(1)

更新节点：O(1)

删除节点：O(1)

优缺点

• 优势

插入、删除、更新效率高

省空间

• 劣势

查询效率较低，不能随机访问

应用

链表的应用也非常广泛，比如树、图、Redis的列表、LRU算法实现、消息队列等。

数组与链表的对比

数据结构没有绝对的好与坏，数组和链表各有千秋。

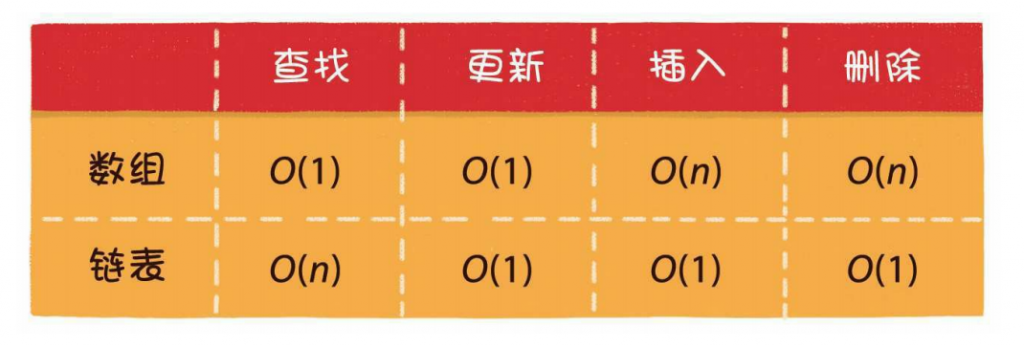
数组的优势在于能够快速定位元素，对于读操作多、写操作少的场景来说，用数组更合适一些。

链表的优势在于能够灵活地进行插入和删除操作，如果需要在尾部频繁插入、删除元素，用链表更合适一些。

数组和链表是线性数据存储的物理存储结构：即顺序存储和链式存储。

栈

栈和队列都属于线性数据的逻辑存储结构。

概念

栈（stack）是一种线性数据结构，栈中的元素只能先入后出（First In Last Out，简称FILO）。

最早进入的元素存放的位置叫作栈底（bottom），最后进入的元素存放的位置叫作栈顶 （top）。

存储原理

栈既可以用数组来实现，也可以用链表来实现。

栈的数组实现如下：

数组实现的栈也叫顺序栈或静态栈。

栈的链表实现如下：

链表实现的栈也叫做链式栈或动态栈。

操作

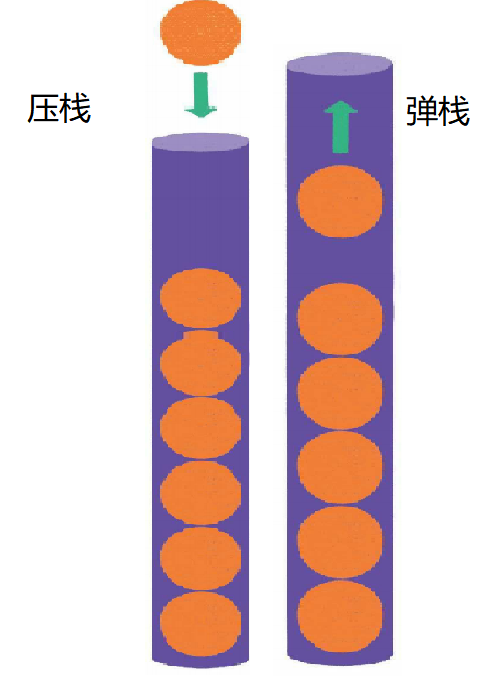
• 入栈（压栈）

入栈操作（push）就是把新元素放入栈中，只允许从栈顶一侧放入元素，新元素的位置将会成为新的栈顶：

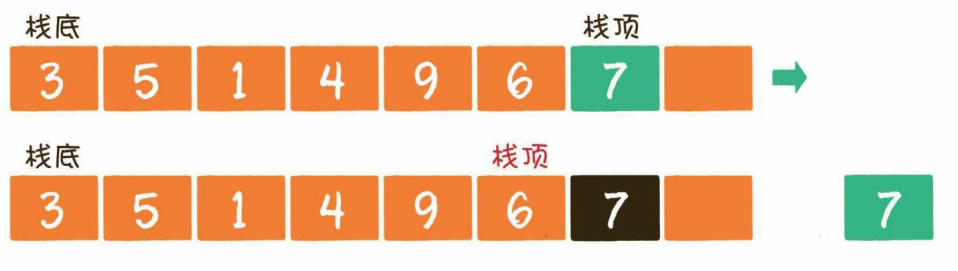
• 出栈（弹栈）

出栈操作（pop）就是把元素从栈中弹出，只有栈顶元素才允许出栈，出栈元素的前一个元素将会成为新的栈顶：

完整代码：

数组实现：

package com.rubin.datastructure.stack;

public class RubinArrayStack {

    private int[] items;

    private int size;

    public RubinArrayStack(int cap) {
        items = new int[cap];
        size = 0;
    }

    public boolean push(int item) {
        if (size == items.length) {
            return false;
        }
        items[size] = item;
        ++size;
        return true;
    }

    public int pop() {
        if (size == 0) {
            return 0;
        }
        --size;
        return items[size];
    }

    public static void main(String[] args) {
        RubinArrayStack rubinArrayStack = new RubinArrayStack(10);
        rubinArrayStack.push(3);
        rubinArrayStack.push(1);
        rubinArrayStack.push(5);
        rubinArrayStack.push(2);
        rubinArrayStack.push(7);
        System.out.println(rubinArrayStack.pop());
        System.out.println(rubinArrayStack.pop());
        System.out.println(rubinArrayStack.pop());
        System.out.println(rubinArrayStack.pop());
        System.out.println(rubinArrayStack.pop());
    }

}

链表实现：

package com.rubin.datastructure.stack;

public class RubinLinkedStack {

    private RubinStackNode head;
    private int size;

    public RubinLinkedStack() {
        size = 0;
    }

    public void push(int item) {
        if (size == 0) {
            head = new RubinStackNode(item);
        } else {
            RubinStackNode newHead = new RubinStackNode(item);
            newHead.next = head;
            head = newHead;
        }
        ++size;
    }

    public int pop() {
        if (size == 0) {
            return 0;
        }
        RubinStackNode oldHead = head;
        head = head.next;
        --size;
        return oldHead.value;
    }

    static class RubinStackNode {
        int value;
        RubinStackNode next;
        public RubinStackNode(int value) {
            this.value = value;
        }
    }

    public static void main(String[] args) {
        RubinLinkedStack rubinLinkedStack = new RubinLinkedStack();
        rubinLinkedStack.push(1);
        rubinLinkedStack.push(2);
        rubinLinkedStack.push(3);
        rubinLinkedStack.push(4);
        rubinLinkedStack.push(5);
        System.out.println(rubinLinkedStack.pop());
        System.out.println(rubinLinkedStack.pop());
        System.out.println(rubinLinkedStack.pop());
        System.out.println(rubinLinkedStack.pop());
        System.out.println(rubinLinkedStack.pop());
    }

}

时间复杂度

入栈和出栈的时间复杂度都是O(1)

支持动态扩容的顺序栈

当数组空间不够时，我们就重新申请一块更大的内存，将原来数组中数据统统拷贝过去。这样就实现了一个支持动态扩容的数组，入栈的时间复杂度是O(n)。

应用

• 函数调用

每进入一个函数，就会将临时变量作为一个栈入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

• 浏览器的后退功能

我们使用两个栈，X 和 Y，我们把首次浏览的页面依次压入栈 X，当点击后退按钮时，再依次从栈X 中出栈，并将出栈的数据依次放入栈 Y。当我们点击前进按钮时，我们依次从栈 Y 中取出数据，放入栈 X 中。当栈 X 中没有数据时，那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据，那就说明没有页面可以点击前进按钮浏览了。

队列

概念

队列（queue）是一种线性数据结构，队列中的元素只能先入先出（First In First Out，简称 FIFO）。队列的出口端叫作队头（front），队列的入口端叫作队尾（rear）。

存储原理

队列这种数据结构既可以用数组来实现，也可以用链表来实现。

• 数组实现

用数组实现时，为了入队操作的方便，把队尾位置规定为最后入队元素的下一个位置。

用数组实现的队列叫作顺序队列。

• 链表实现

用链表实现的队列叫作链式队列。

操作

• 入队

入队（enqueue）就是把新元素放入队列中，只允许在队尾的位置放入元素，新元素的下一个位置将会成为新的队尾：

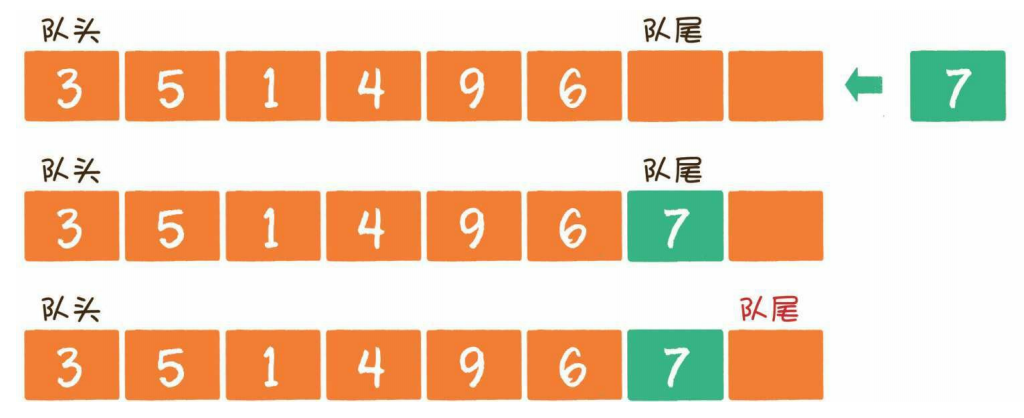
• 出队

出队操作（dequeue）就是把元素移出队列，只允许在队头一侧移出元素，出队元素的后一个元素将会成为新的队头：

完整代码：

数组实现：

package com.rubin.datastructure.queue;

public class RubinArrayQueue {

    private int[] items;

    private int head, tail;

    private int size;

    public RubinArrayQueue(int cap) {
        items = new int[cap];
        head = tail = size = 0;
    }

    public boolean enqueue(int item) {
        if (size == items.length) {
            return false;
        }
        items[tail] = item;
        ++size;
        ++tail;
        if (tail == items.length) {
            tail = 0;
        }
        return true;
    }

    public int dequeue() {
        if (size == 0) {
            return 0;
        }
        int result = items[head];
        --size;
        ++head;
        if (head == items.length) {
            head = 0;
        }
        return result;
    }

    public static void main(String[] args) {
        RubinArrayQueue rubinArrayQueue = new RubinArrayQueue(10);
        for (int i = 0; i < 10; i++) {
            rubinArrayQueue.enqueue(i);
        }
        for (int j = 0; j < 10; j++) {
            System.out.println(rubinArrayQueue.dequeue());
        }
    }

}

链表实现：

package com.rubin.datastructure.queue;

public class RubinLinkedQueue {

    private RubinQueueNode head;
    private RubinQueueNode tail;

    private int size;

    public RubinLinkedQueue() {
        head = tail = null;
        size = 0;
    }

    static class RubinQueueNode {
        int value;
        RubinQueueNode next;
        public RubinQueueNode(int value) {
            this.value = value;
        }
    }

    public void enqueue(int item) {
        if (size == 0) {
            head = tail = new RubinQueueNode(item);
        } else {
            RubinQueueNode newTail = new RubinQueueNode(item);
            tail.next = newTail;
            tail = newTail;
        }
        ++size;
    }

    public int dequeue() {
        if (size == 0) {
            return 0;
        }
        RubinQueueNode h = head;
        int result = h.value;
        head = head.next;
        --size;
        h.next = null;
        return result;
    }

    public static void main(String[] args) {
        RubinLinkedQueue rubinLinkedQueue = new RubinLinkedQueue();
        for (int i = 0; i < 10; i++) {
            rubinLinkedQueue.enqueue(i);
        }
        for (int j = 0; j < 10; j++) {
            System.out.println(rubinLinkedQueue.dequeue());
        }
    }

}

时间复杂度

入队和出队都是O(1)。

应用

资源池、消息队列、命令队列等等。

以上就是本文的全部内容。欢迎各位小伙伴积极留言交流~~~