概念

二分查找（Binary Search）算法，也叫折半查找算法

当我们要从一个序列中查找一个元素的时候，二分查找是一种非常快速的查找算法

二分查找是针对有序数据集合的查找算法，如果是无序数据集合就遍历查找

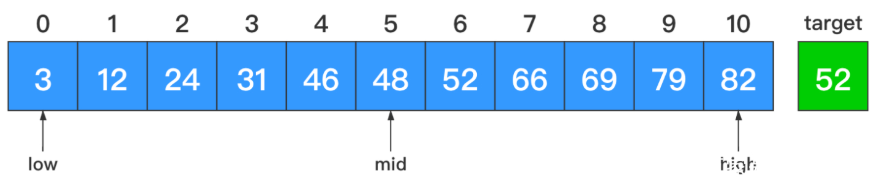
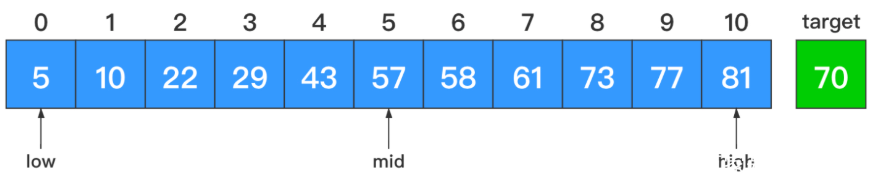
本质

二分查找之所以快速，是因为它在匹配不成功的时候，每次都能排除剩余元素中一半的元素。因此可能包含目标元素的有效范围就收缩得很快，而不像顺序查找那样，每次仅能排除一个元素。

小例子

一个有序的数组中查找某个数字是否存在：

package com.rubin.algorithm.search;

public class BinarySearch {

    /**
     * 经典二分查找
     *
     * @param nums
     * @param item
     * @return
     */
    public static int normalBinarySearch(int[] nums, int item) {
        int low = 0, high = nums.length - 1, mid;
        while (low <= high) {
            mid = (low + high) / 2;
            int midValue = nums[mid];
            if (midValue == item) {
                return mid;
            } else if (midValue > item) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        return -1;
    }

    /**
     * 递归二分查找
     *
     * @param nums
     * @param item
     * @return
     */
    public static int recursionBinarySearch(int[] nums, int item) {
        return doRecursionBinarySearch(nums, item, 0, nums.length - 1);
    }

    private static int doRecursionBinarySearch(int[] nums, int item, int low, int high) {
        if (low > high) {
            return -1;
        }
        int mid = (low + high) / 2;
        int midValue = nums[mid];
        if (midValue == item) {
            return mid;
        } else if (midValue > item) {
            return doRecursionBinarySearch(nums, item, low, mid - 1);
        } else {
            return doRecursionBinarySearch(nums, item, mid + 1, high);
        }
    }

    /**
     * 一个有序数组有一个数出现1次，其他数出现2次，找出出现一次的数
     *
     * @param nums
     * @return
     */
    public static int onceBinarySearch(int[] nums) {
        int low = 0, high = nums.length - 1, mid;
        while (low < high) {
            mid = (low + high) / 2;
            // 偶数位
            if (mid % 2 == 0) {
                // 偶数位跟后面的相等 说明前面的都对
                if (nums[mid] == nums[mid + 1]) {
                    low = mid + 1;
                }
                // 偶数位跟前面的相等 说明后面的都对
                else if (nums[mid] == nums[mid - 1]) {
                    high = mid - 1;
                }
                // 前后都不相等 就是该数
                else {
                    return nums[mid];
                }
            }
            // 奇数位
            else {
                // 奇数位跟后面的相等 说明后的都对
                if (nums[mid] == nums[mid + 1]) {
                    high = mid - 1;
                }
                // 奇数位跟前面的相等 说明前的都对
                else if (nums[mid] == nums[mid - 1]) {
                    low = mid + 1;
                }
                // 前后都不相等 就是该数
                else {
                    return nums[mid];
                }
            }
        }
        // low == high
        return nums[low];
    }

    public static void main(String[] args) {
        int[] nums = {2, 4, 5, 7, 10, 24, 36, 89};
        System.out.println(normalBinarySearch(nums, 5));
        System.out.println(recursionBinarySearch(nums, 2));
        int[] onceNums = {1, 1, 2, 2, 3, 4, 4, 5, 5};
        System.out.println(onceBinarySearch(onceNums));
    }

}