概念
递归,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。也就是说,递归算法是一种直接或者间接调用自身函数或者方法的算法。

本质
递归,去的过程叫"递",回来的过程叫”归“
递是调用,归是结束后回来
是一种循环,而且在循环中执行的就是调用自己
递归调用将每次返回的结果存在栈帧中
递归三要素
- 递归结束条件:既然是循环就必须要有结束,不结束就会OOM了
- 函数的功能:这个函数要干什么,打印,计算….
- 函数的等价关系式:递归公式,一般是每次执行之间,或者与个数之间的逻辑关系
小例子
打印5次”Hello World“
package com.rubin.algorithm.recursion;
public class Print {
public static void main(String[] args) {
print("hello rubin", 5);
}
private static void print(String str, int count) {
if (count <= 0) {
return;
}
System.out.println(str);
print(str, --count);
}
}
递归要素:
- 递归结束条件:n<=0
- 函数的功能:System.out.println(str);
- 函数的等价关系式:fun(n)=fun(n-1)
经典案例
斐波那契数列:0、1、1、2、3、5、8、13、21、34、55…..
规律:从第3个数开始,每个数等于前面两个数的和
递归分析:
- 函数的功能:返回n的前两个数的和
- 递归结束条件:从第三个数开始,n<=2
- 函数的等价关系式:fun(n)=fun(n-1)+fun(n-2)
package com.rubin.algorithm.recursion;
public class Fibonacci {
public static int findFibonacciItem(int index) {
if (index <= 2) {
return index - 1;
}
return findFibonacciItem(index -1) + findFibonacciItem(index - 2);
}
public static void main(String[] args) {
for (int i = 1; i <= 10; i++) {
System.out.print(findFibonacciItem(i) + " ");
}
}
}
时间复杂度
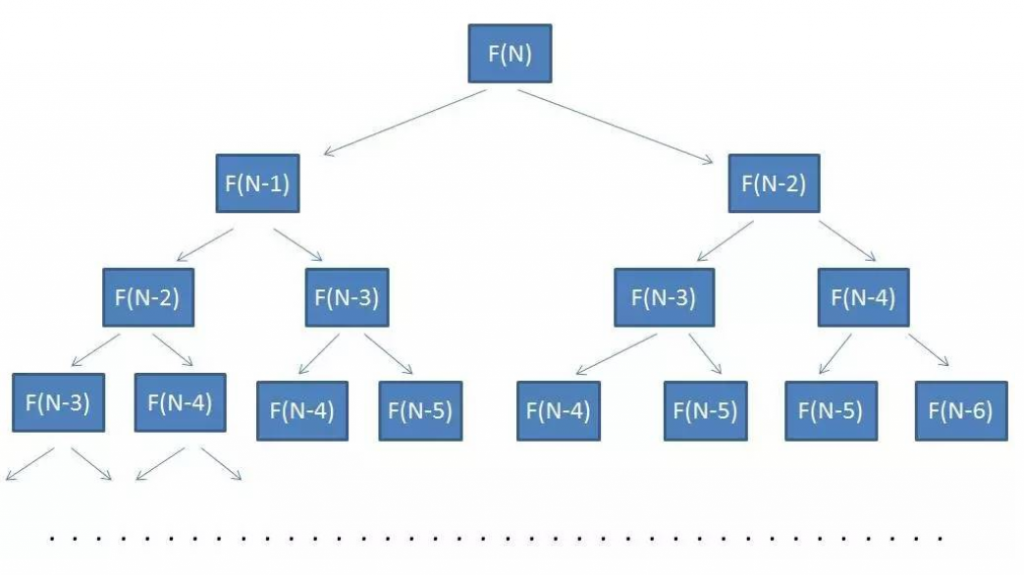
斐波那契数列普通递归解法为:O(2^n)
优缺点
优点:代码简单
缺点:占用空间较大、如果递归太深,可能会发生栈溢出、可能会有重复计算。可通过备忘录或递归的方式去优化
应用
递归作为基础算法,应用非常广泛,比如在二分查找、快速排序、归并排序、树的遍历上都有使用递归
回溯算法、分治算法、动态规划中也大量使用递归算法实现
以上就是本文的全部内容。欢迎小伙伴们积极留言交流~~~
文章评论