树的概念
有很多数据的逻辑关系并不是线性关系,在实际场景中,常常存在着一对多,甚至是多对多的情况。
家谱:
组织结构:
书的目录:
以上的数据结构,我们称为树。
在数据结构中,树的定义如下:
树(tree)是n(n≥0)个节点的有限集。
当n=0时,称为空树。在任意一个非空树中,有如下特点。
有且仅有一个特定的称为根的节点。
当n>1时,其余节点可分为m(m>0)个互不相交的有限集。
每一个集合本身又是一个树,并称为根的子树。
一个标准的树结构:
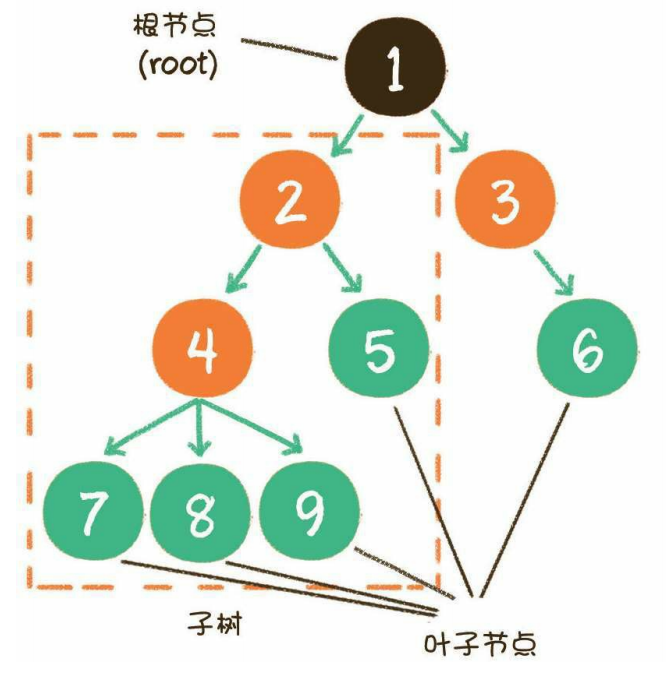
节点1是根节点(root),没有父节点
节点5、6、7、8是树的末端,没有“孩子”,被称为叶子节点(leaf)
节点2、3、4、是树的中端,有父节点,有孩子,被称为中间节点或枝节点
图中的虚线部分,是根节点1的其中一个子树
树的最大层级数,被称为树的高度或深度,上图这个树的高度是4
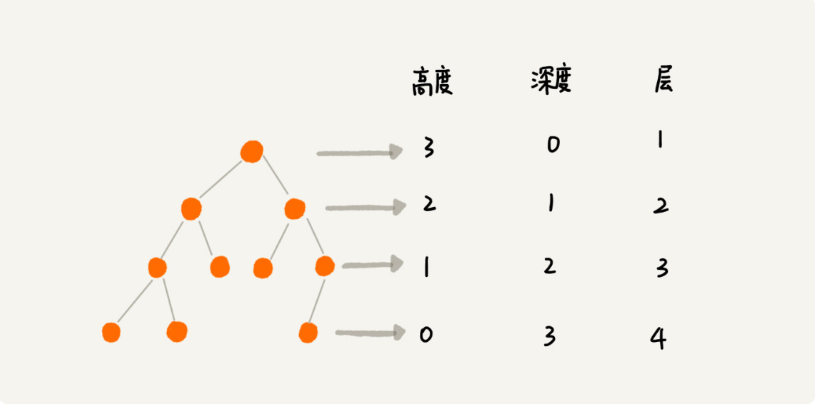
树的分类如下:

树的种类非常多,我们会选几个有代表性的详细讲解。
二叉树
二叉树(binary tree)是树的一种特殊形式。二叉,顾名思义,这种树的每个节点最多有2个孩子节点。注意,这里是最多有2个,也可能只有1个,或者没有孩子节点。

二叉树节点的两个孩子节点,一个被称为左孩子(left child),一个被称为右孩子(right child)。这两个孩子节点的顺序是固定的,左孩子小于右孩子。
- 满二叉树
一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树:

- 完全二叉树
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个二叉树为完全二叉树:
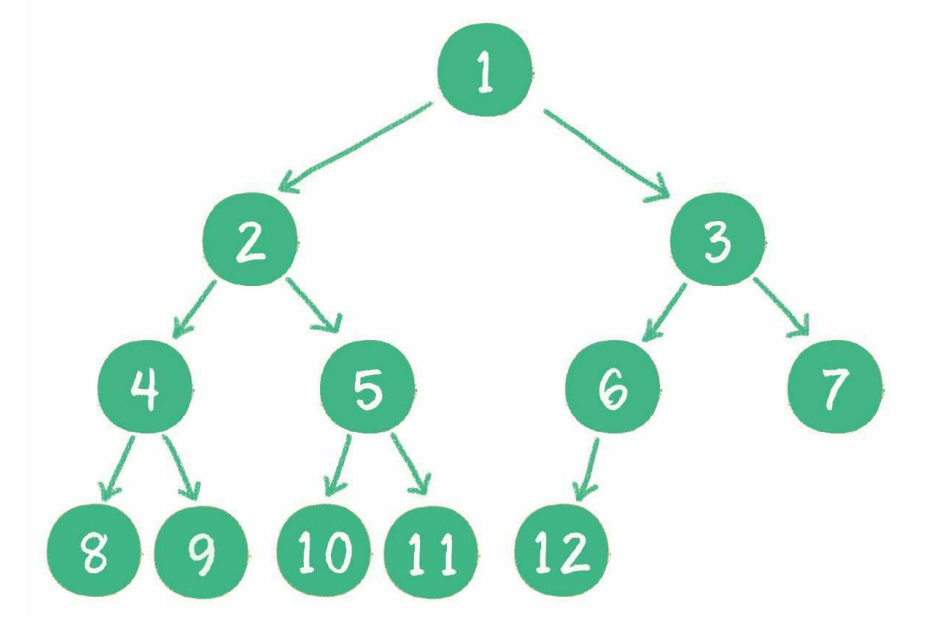
满二叉树要求所有分支都是满的;而完全二叉树只需保证最后一个节点之前的节点都齐全即可。
二叉树的存储
二叉树属于逻辑结构,可以使用链表和数组进行存储。
- 链式存储
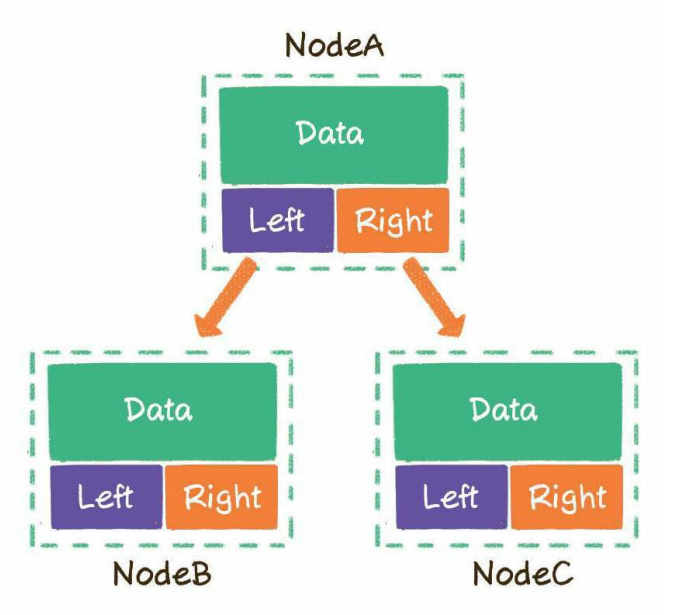
二叉树的每一个节点包含3部分:存储数据的data变量、指向左孩子的left指针、指向右孩子的right指针。
- 数组存储
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。
如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。
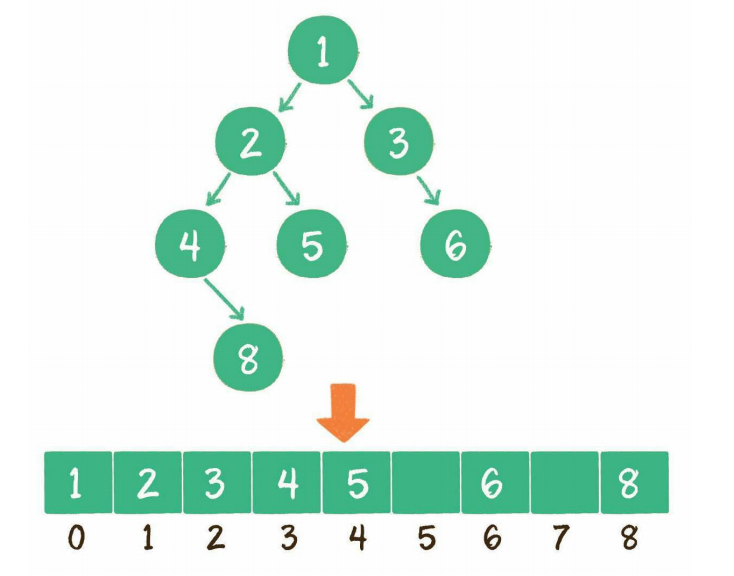
寻址方式:
一个父节点的下标是n,那么它的左孩子节点下标就是2×n+1、右孩子节点下标就是2*(n+1)。
对于一个稀疏的二叉树(孩子不满)来说,用数组表示法是非常浪费空间的。
所以二叉树一般用链表存储实现。(二叉堆除外)
二叉查找树
二叉查找树(binary search tree),二叉查找树在二叉树的基础上增加了以下几个条件:
- 如果左子树不为空,则左子树上所有节点的值均小于根节点的值
- 如果右子树不为空,则右子树上所有节点的值均大于根节点的值
- 左、右子树也都是二叉查找树
如下图:
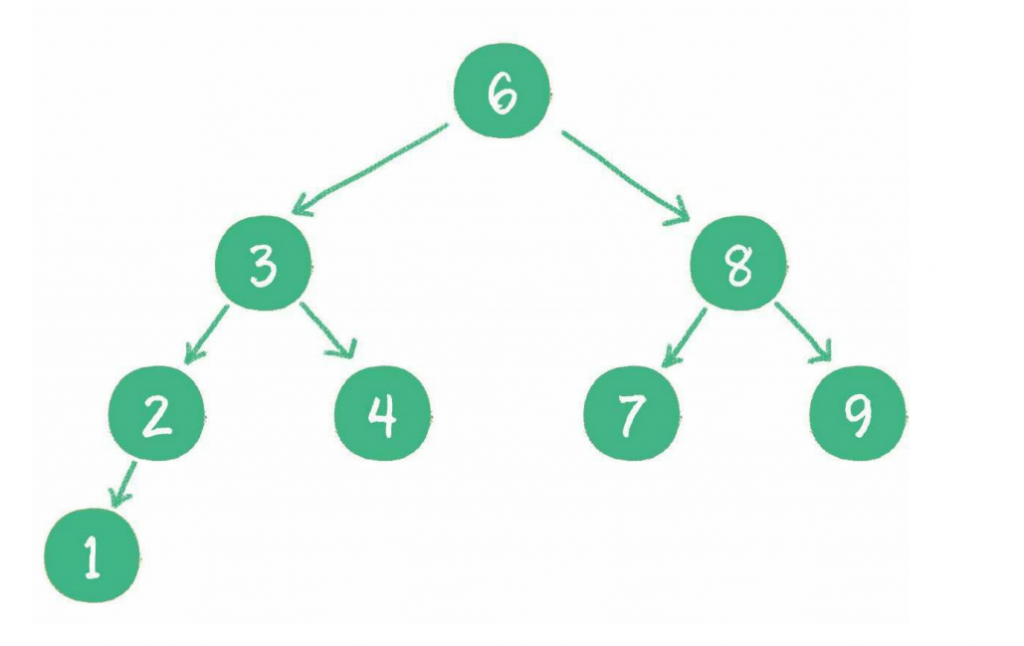
二叉查找树要求左子树小于父节点,右子树大于父节点,正是这样保证了二叉树的有序性。因此二叉查找树还有另一个名字——二叉排序树(binary sort tree)。
查找
例如查找值为4的节点,步骤如下:
- 访问根节点6,发现4<6
- 访问节点6的左孩子节点3,发现4>3
- 访问节点3的右孩子节点4,发现4=4,这正是要查找的节点
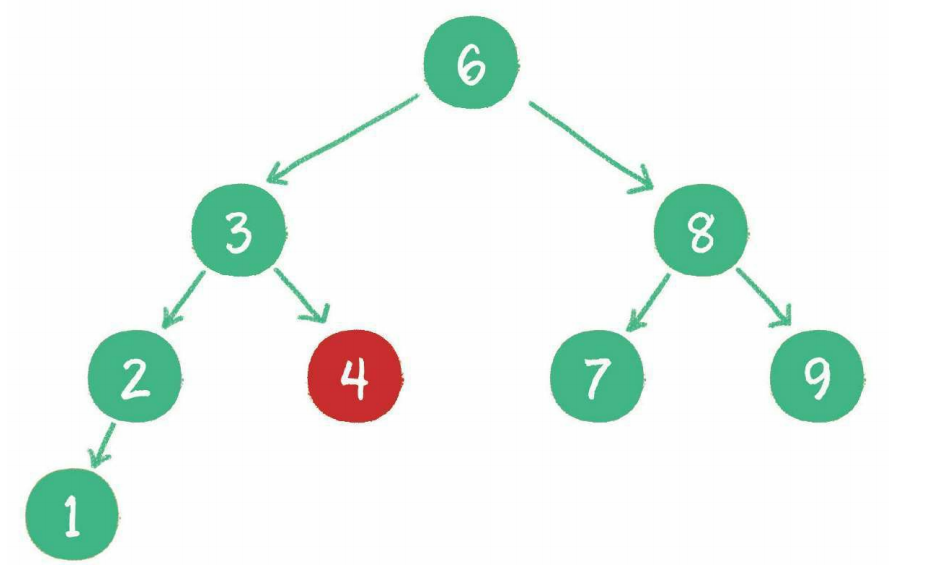
对于一个节点分布相对均衡的二叉查找树来说,如果节点总数是n,那么搜索节点的时间复杂度就是O(logn),和树的深度是一样的。这种方式正是二分查找思想。
插入
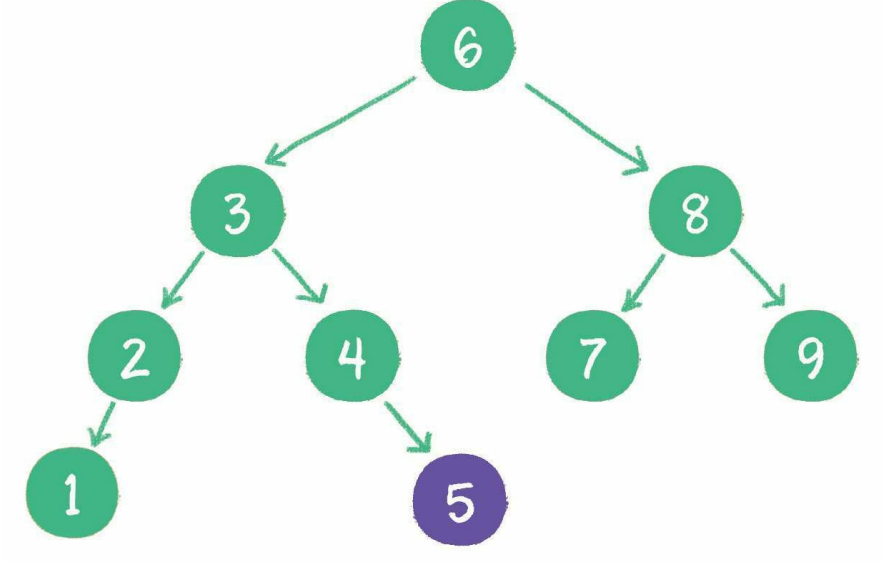
例如插入新元素5,步骤如下:
- 访问根节点6,发现5<6
- 访问节点6的左孩子节点3,发现5>3
- 访问节点3的右孩子节点4,发现5>4
- 5最终会插入到节点4的右孩子位置
二叉树的遍历
二叉树,是典型的非线性数据结构,遍历时需要把非线性关联的节点转化成一个线性的序列,以不同的方式来遍历,遍历出的序列顺序也不同。
深度优先遍历
所谓深度优先,顾名思义,就是偏向于纵深,“一头扎到底”的访问方式。它包括:
前序遍历
二叉树的前序遍历,输出顺序是根节点、左子树、右子树:

步骤如下:
- 首先输出的是根节点1
- 由于根节点1存在左孩子,输出左孩子节点2
- 由于节点2也存在左孩子,输出左孩子节点4
- 节点4既没有左孩子,也没有右孩子,那么回到节点2,输出节点2的右孩子节点5
- 节点5既没有左孩子,也没有右孩子,那么回到节点1,输出节点1的右孩子节点3
- 节点3没有左孩子,但是有右孩子,因此输出节点3的右孩子节点6
到此为止,所有的节点都遍历输出完毕。
中序遍历
二叉树的中序遍历,输出顺序是左子树、根节点、右子树:
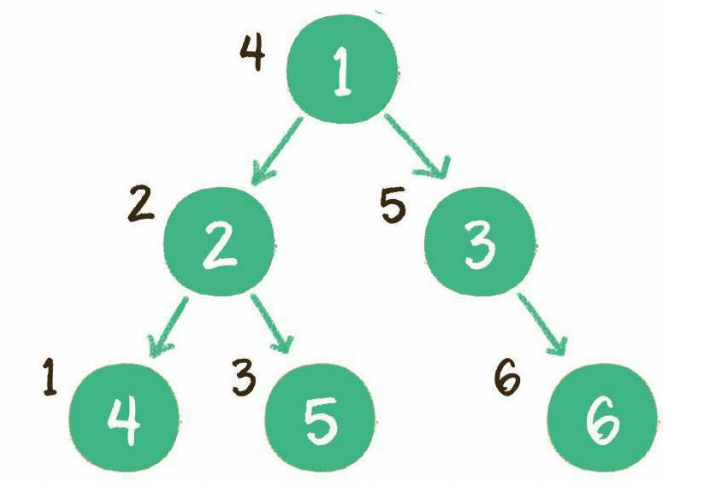
步骤如下:
- 首先访问根节点的左孩子,如果这个左孩子还拥有左孩子,则继续深入访问下去,一直找到不再有左孩子 的节点,并输出该节点。显然,第一个没有左孩子的节点是节点4
- 依照中序遍历的次序,接下来输出节点4的父节点2
- 再输出节点2的右孩子节点5
- 以节点2为根的左子树已经输出完毕,这时再输出整个二叉树的根节点1
- 由于节点3没有左孩子,所以直接输出根节点1的右孩子节点3
- 最后输出节点3的右孩子节点6
到此为止,所有的节点都遍历输出完毕。
后序遍历
二叉树的后序遍历,输出顺序是左子树、右子树、根节点:

步骤如下:
- 首先访问根节点的左孩子,如果这个左孩子还拥有左孩子,则继续深入访问下去,一直找到不再有左孩子的节点,并输出该节点。显然,第一个没有左孩子的节点是节点4
- 输出右节点5
- 输出节点4的父节点2
- 以节点2为根的左子树已经输出完毕,这时再输出整个二叉树的右子树
- 访问根节点的右孩子,如果这个右孩子拥有左孩子,则继续深入访问下去,一直找到不再有左孩子的节点,如果没有左孩子则找右孩子,并输出该节点6
- 输出节点6的父节点3
到此为止,所有的节点都遍历输出完毕。
代码如下:
package com.rubin.datastructure.tree;
import java.util.LinkedList;
import java.util.Queue;
/**
* 二叉排序树
*/
public class RubinBinarySortTree {
private BinarySortTreeNode root;
static class BinarySortTreeNode {
int value;
BinarySortTreeNode left;
BinarySortTreeNode right;
public BinarySortTreeNode(int value) {
this.value = value;
}
}
/**
* 添加节点
*
* @param value
*/
public void insert(int value) {
root = insert(root, value);
}
private BinarySortTreeNode insert(BinarySortTreeNode node, int value) {
if (node == null) {
return new BinarySortTreeNode(value);
}
if (value < node.value) {
node.left = insert(node.left, value);
} else if (value > node.value) {
node.right = insert(node.right, value);
} else {
node.value = value;
}
return node;
}
/**
* 前序遍历
* 根节点 -> 左子树 -> 右子树
*/
public void preOrderTraveral() {
doPreOrderTraveral(root);
}
private void doPreOrderTraveral(BinarySortTreeNode node) {
if (node == null) {
return;
}
System.out.print(node.value + " ");
doPreOrderTraveral(node.left);
doPreOrderTraveral(node.right);
}
/**
* 中序便利
* 左子树 -> 根节点 -> 右子树
*/
public void midOrderTraveral() {
doMidOrderTraveral(root);
}
private void doMidOrderTraveral(BinarySortTreeNode node) {
if (node == null) {
return;
}
doMidOrderTraveral(node.left);
System.out.print(node.value + " ");
doMidOrderTraveral(node.right);
}
/**
* 后序便利
* 左子树 -> 右子树 -> 根节点
*/
public void postOrderTraveral() {
doPostOrderTraveral(root);
}
private void doPostOrderTraveral(BinarySortTreeNode node) {
if (node == null) {
return;
}
doPostOrderTraveral(node.left);
doPostOrderTraveral(node.right);
System.out.print(node.value + " ");
}
/**
* 层序遍历
*/
public void levelOrderTraversal() {
Queue<BinarySortTreeNode> queue = new LinkedList<BinarySortTreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
BinarySortTreeNode node = queue.poll();
System.out.print(node.value + " ");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
public static void main(String[] args) {
RubinBinarySortTree tree = new RubinBinarySortTree();
tree.insert(6);
tree.insert(5);
tree.insert(10);
tree.insert(3);
tree.insert(8);
tree.insert(1);
tree.insert(56);
System.out.println("pre");
tree.preOrderTraveral();
System.out.println();
System.out.println("mid");
tree.midOrderTraveral();
System.out.println();
System.out.println("post");
tree.postOrderTraveral();
System.out.println();
System.out.println("level");
tree.levelOrderTraversal();
}
}
广度优先遍历
也叫层序遍历,顾名思义,就是二叉树按照从根节点到叶子节点的层次关系,一层一层横向遍历各个节点。
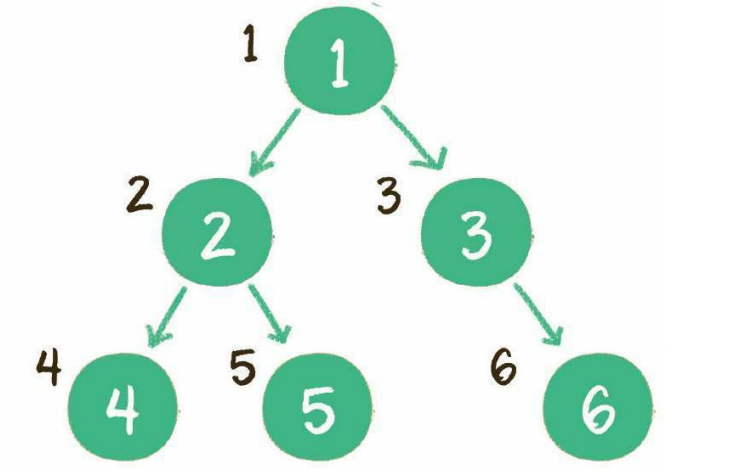
二叉树同一层次的节点之间是没有直接关联的,利用队列可以实现。
1、根节点1进入队列
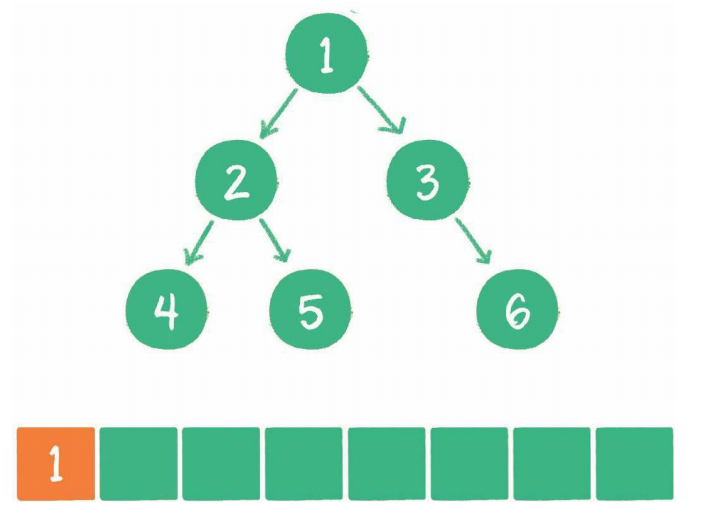
2、节点1出队,输出节点1,并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队
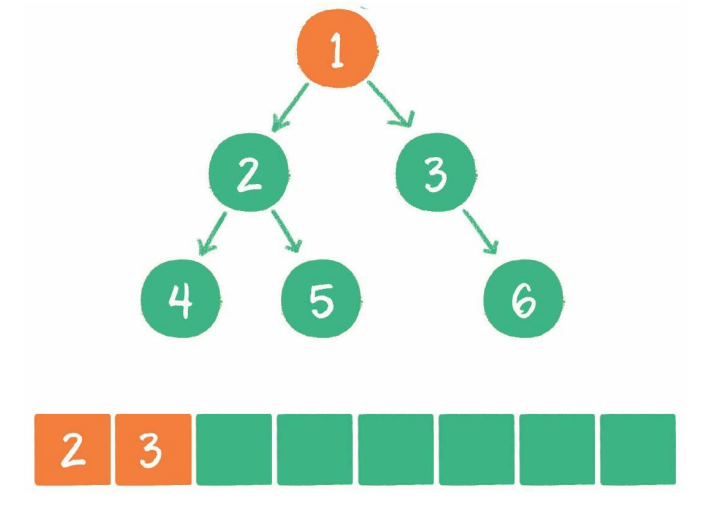
3、节点2出队,输出节点2,并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队
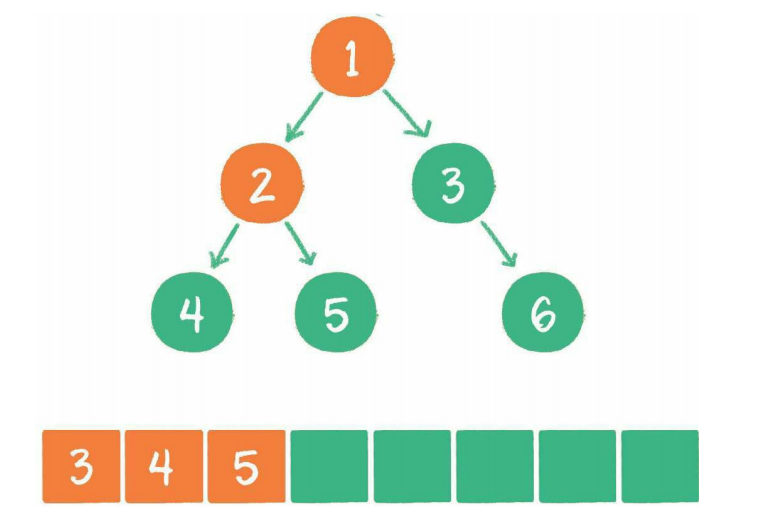
4、节点3出队,输出节点3,并得到节点3的右孩子节点6。让节点6入队
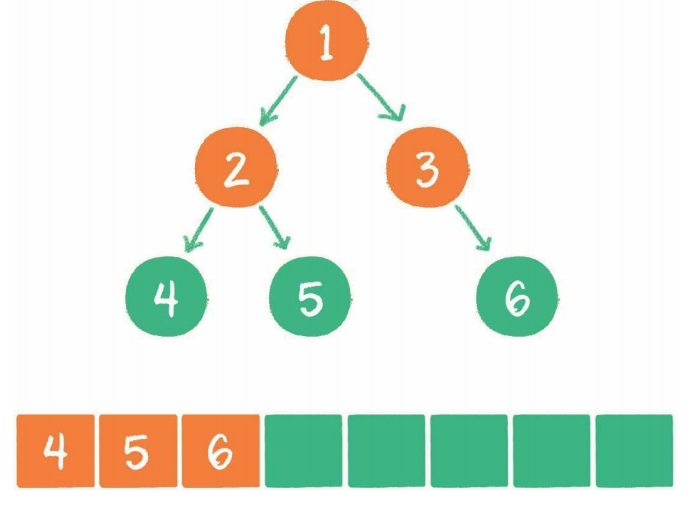
5、节点4出队,输出节点4,由于节点4没有孩子节点,所以没有新节点入队
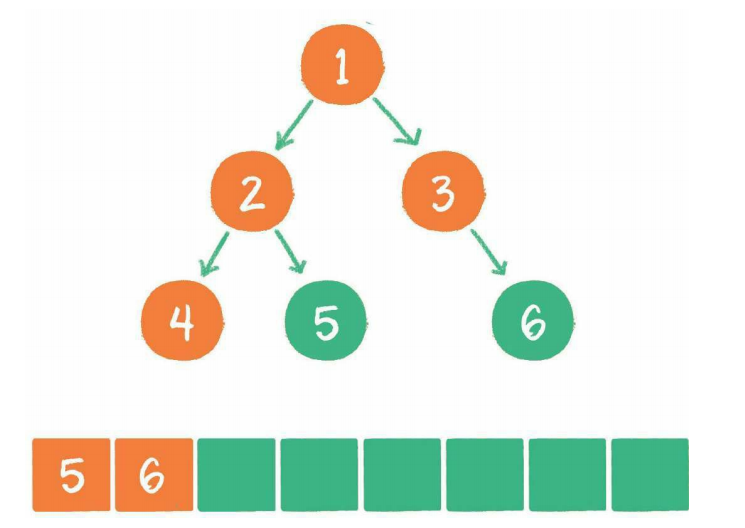
6、节点5出队,输出节点5,由于节点5同样没有孩子节点,所以没有新节点入队

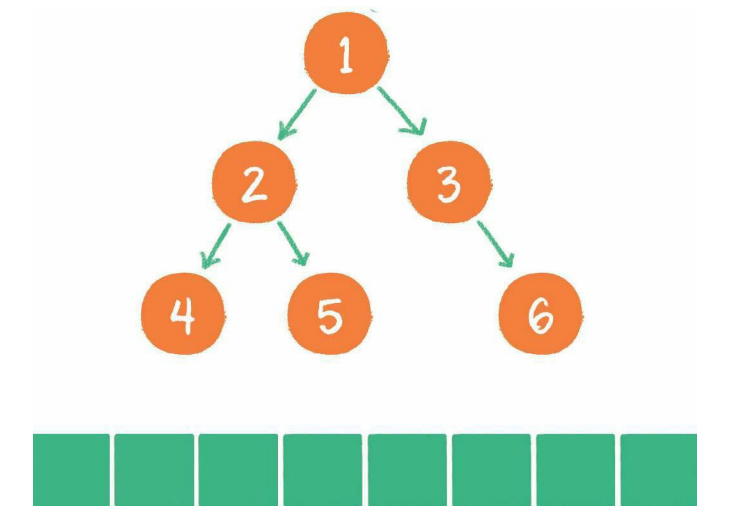
7、节点6出队,输出节点6,节点6没有孩子节点,没有新节点入队
/**
* 层序遍历
*/
public void levelOrderTraversal() {
Queue<BinarySortTreeNode> queue = new LinkedList<BinarySortTreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
BinarySortTreeNode node = queue.poll();
System.out.print(node.value + " ");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}时间复杂度
二叉查找树的插入和查找时间复杂度为:O(logn)
极端情况下二叉查找树退化成链表,时间复杂度为O(n),所以需要平衡二叉查找树
应用
非线性数据:菜单,组织结构、家谱等等
线性数据:二叉查找树
二叉查找树是有序的,我们只需要中序遍历,就可以在 O(n) 的时间复杂度内,输出有序的数据序列
二叉查找树的性能非常稳定,扩容很方便(链表实现)
红黑树
平衡二叉查找树在极端情况下会退化成链表:
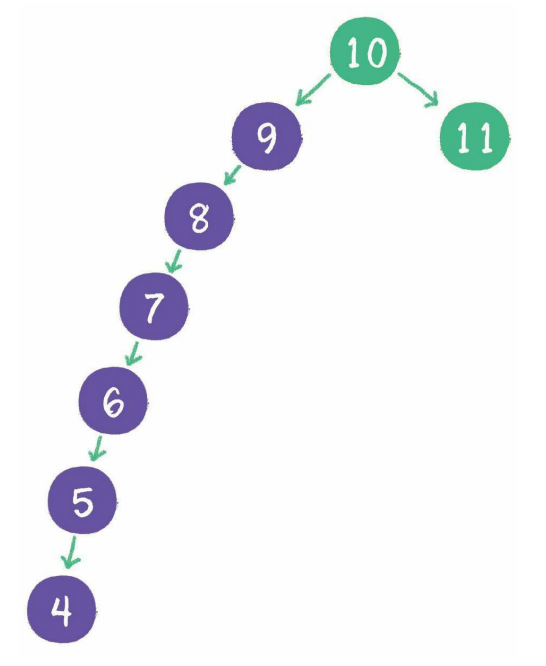
查找的效率也会大幅下降。所以需要对这种二叉树进行自平衡,红黑树就是一种自平衡的二叉查找树。
红黑树(Red Black Tree)除了二叉查找树(BST)的特征外,还有以下特征:
- 每个节点要么是黑色,要么是红色
- 根节点是黑色
- 每个叶子节点都是黑色的空节点(NIL节点)(为了简单期间,一般会省略该节点)
- 如果一个节点是红色的,则它的子节点必须是黑色的(父子不能同为红)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(平衡的关键)
- 新插入节点默认为红色,插入后需要校验红黑树是否符合规则,不符合则需要进行平衡
一颗典型的红黑树:
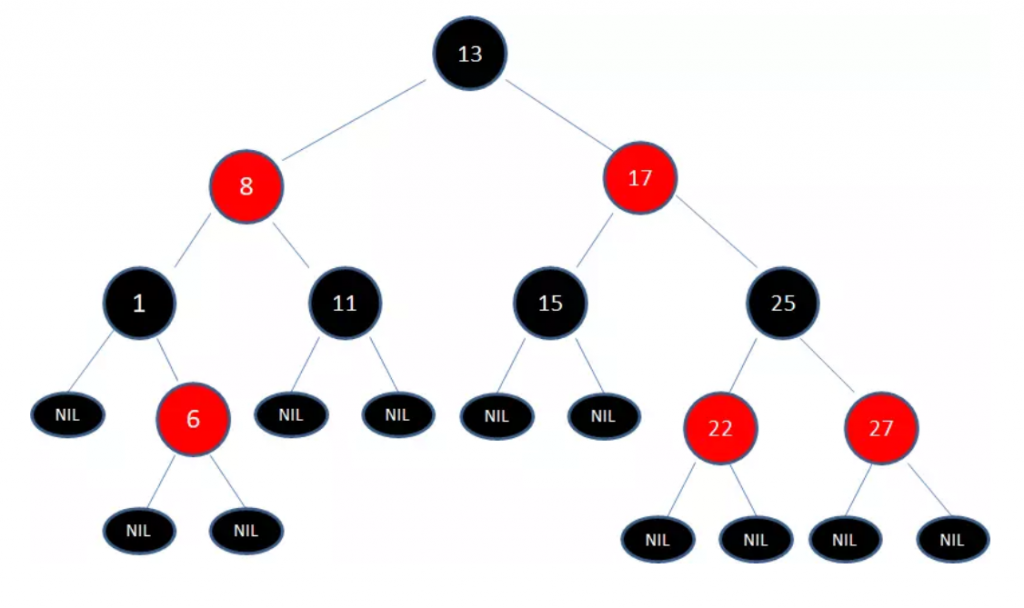
在对红黑树进行添加或者删除操作时可能会破坏这些特点,所以红黑树采取了很多方式来维护这些特点,从而维持平衡。主要包括:左旋转、右旋转和颜色反转。
左旋(RotateLeft)
逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子:
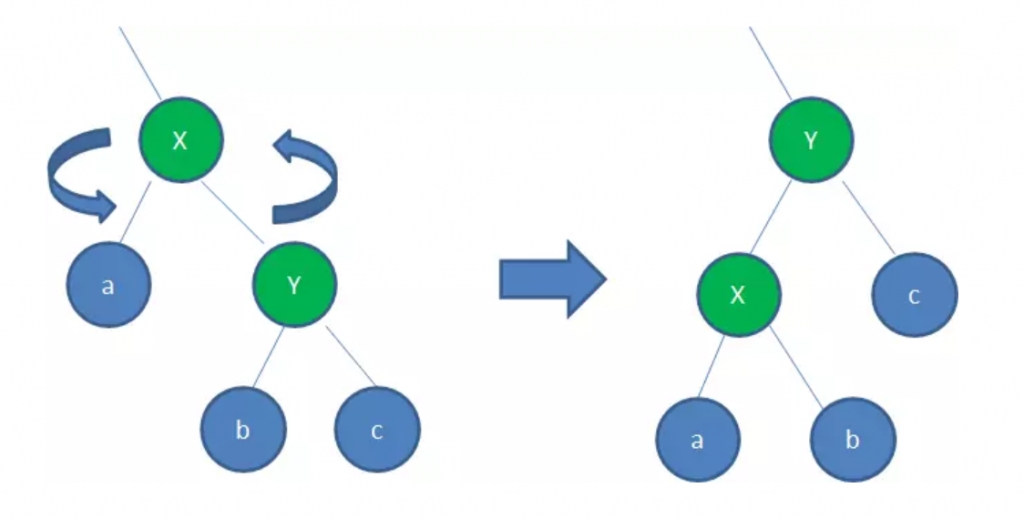
上图所示过程如下:
- 以X为基点逆时针旋转
- X的父节点被x原来的右孩子Y取代
- c保持不变
- Y节点原来的左孩子c变成X的右孩子
右旋(RotateRight)
顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子:
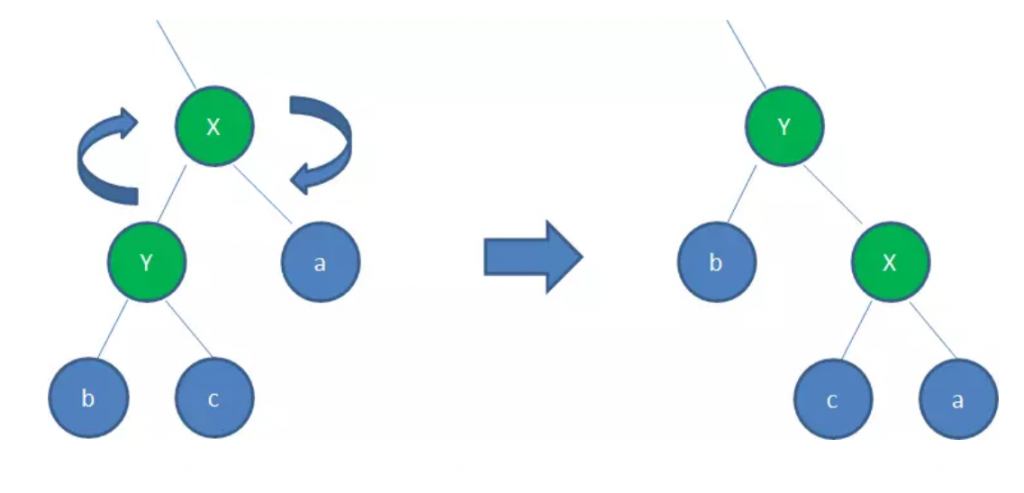
上图所示过程如下:
- 以X为基点顺时针旋转
- X的父节点被x原来的左孩子Y取代
- b保持不变
- Y节点原来的右孩子c变成X的左孩子
颜色反转
就是当前节点与父节点、叔叔节点同为红色,这种情况违反了红黑树的规则,需要将红色向祖辈上传,父节点和叔叔节点红色变为黑色,爷爷节点从黑色变为红色(爷爷节点必为黑色,因为此前是符合红黑树规则的)。这样每条叶子节点到根节点的黑色节点数量并未发生变化,因此都其他树结构不产生影响:
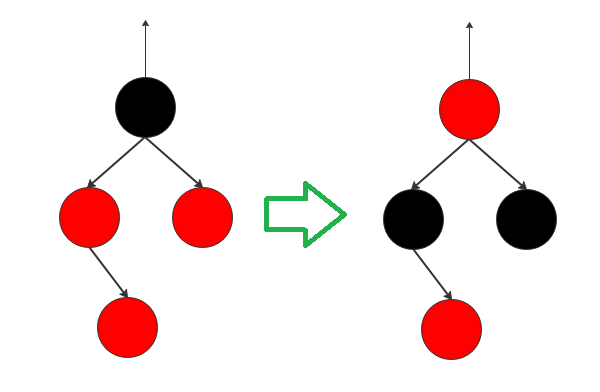
插入
红黑树插入有五种情况,每种情况对应着不同的调整方法:
- 新节点(A)位于树根,没有父节点
直接让新节点变色为黑色,规则2得到满足。同时,黑色的根节点使得每条路径上的黑色节点数目都增加了1,所以并没有打破规则5:
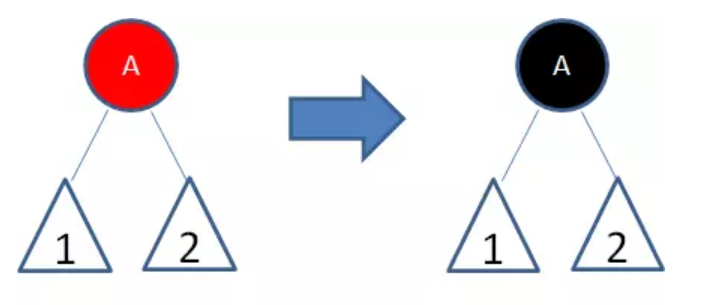
- 新节点(B)的父节点是黑色
新插入的红色节点B并没有打破红黑树的规则,所以不需要做任何调整:
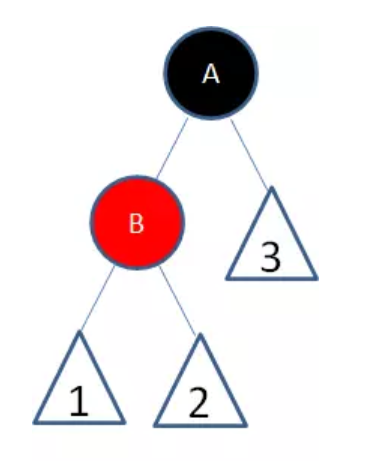
- 新节点(D)的父节点和叔叔节点都是红色
两个红色节点B和D连续,违反了规则4。因此我们先让节点B变为黑色:
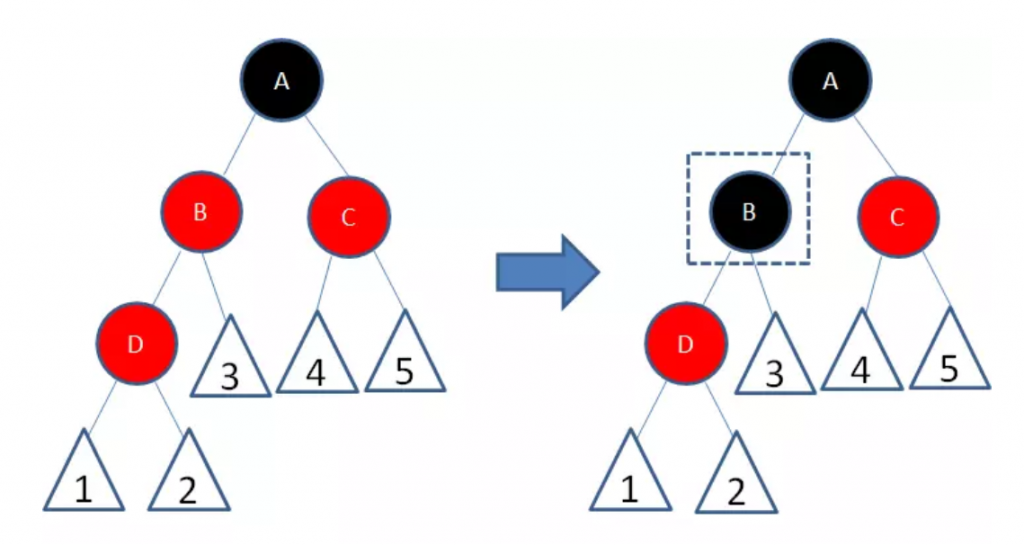
这样一来,节点B所在路径凭空多了一个黑色节点,打破了规则5。因此我们让节点A变为红色:
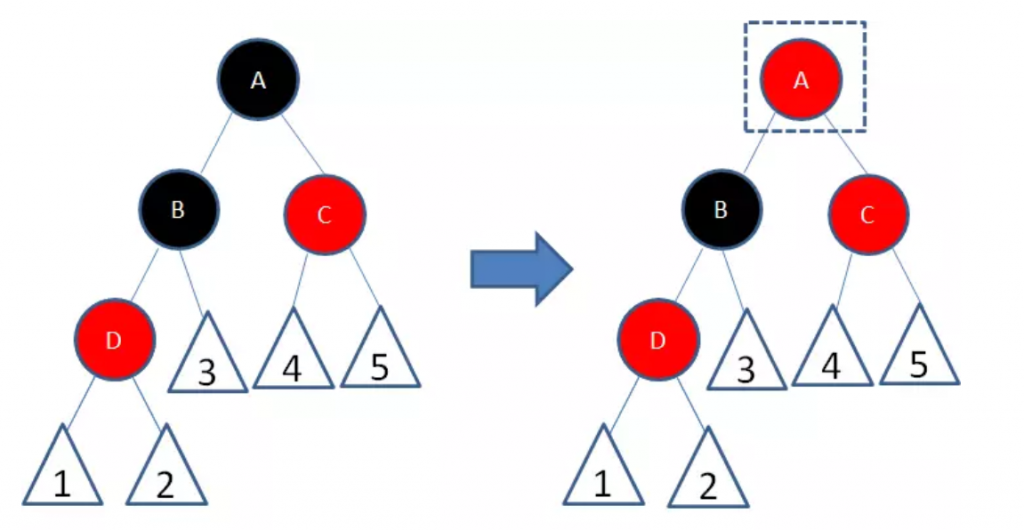
节点A和C又成为了连续的红色节点,我们再让节点C变为黑色:
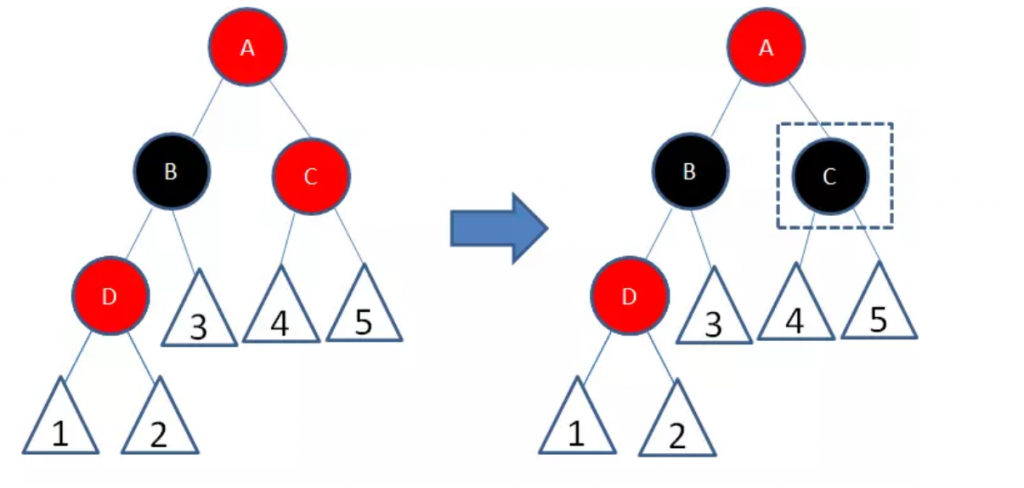
经过上面的调整,这一局部重新符合了红黑树的规则。
- 新节点(D)的父节点是红色,叔叔节点是黑色或者没有叔叔,且新节点是父节点的右孩子,父节点(B)是祖父节点的左孩子
我们以节点B为轴,做一次左旋转,使得新节点D成为父节点,原来的父节点B成为D的左孩子:
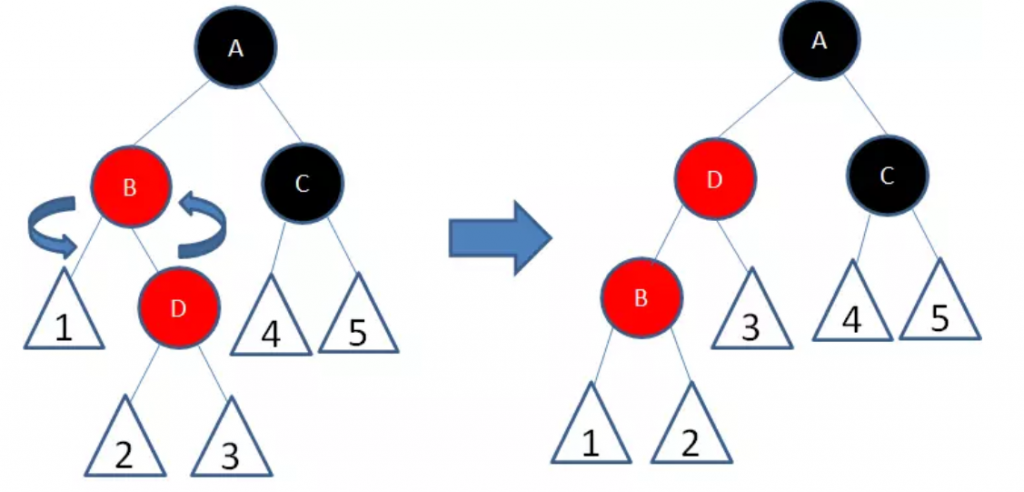
这样进入了下面的情况。
- 新节点(D)的父节点是红色,叔叔节点是黑色或者没有叔叔,且新节点是父节点的左孩子,父节点(B)是祖父节点的左孩子
我们以节点为轴,做一次右旋转,使得节点B成为祖父节点,节点A成为节点B的右孩子:

接下来,我们让节点B变为黑色,节点A变为红色:
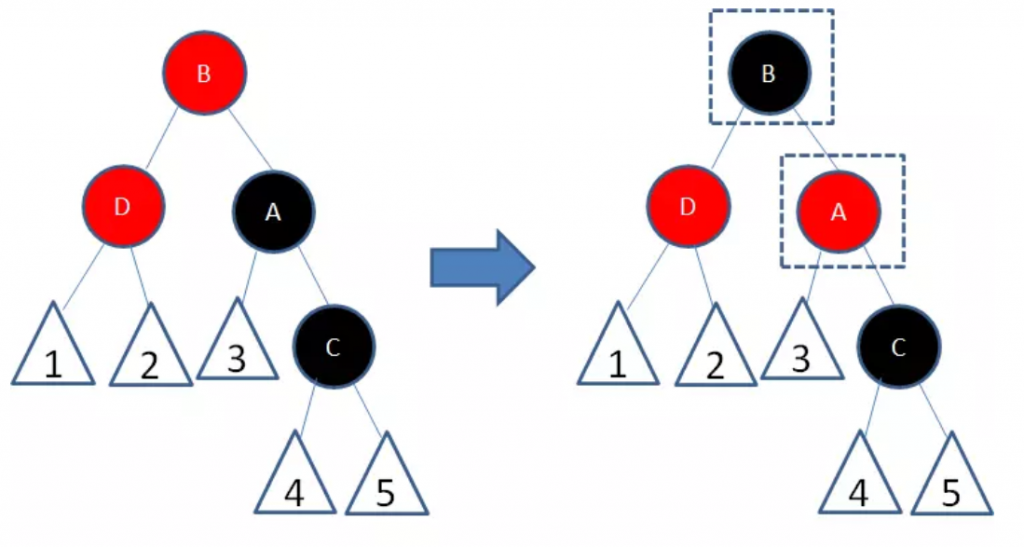
经过上面的调整,这一局部重新符合了红黑树的规则。
红黑树构建过程
如下图:
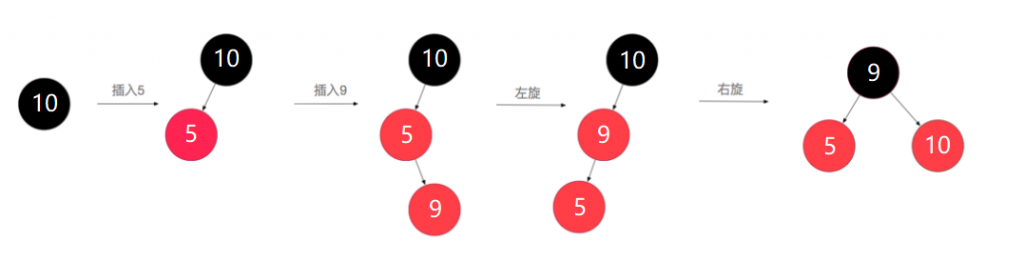
上图所示过程如下:
1、新插入节点默认为红色,5<10,插入到左子节点,插入后左子树深度为2(叶子节点黑色+根节点黑色),右子树深度为也是2(叶子节点黑色+根节点黑色),满足红黑树规则
2、新插入节点为红色,9<10,需要在左子树进行插入,再和5比较,大于5,放到5的右子树中,此时各个叶子节点到根节点的深度依然是2,但5和9两个节点都是红色,不满足规则第4条,需要进行左旋、右旋操作,使其符合规则。可以看出经过操作后,左右子树又维持了平衡
上图所示过程如下:
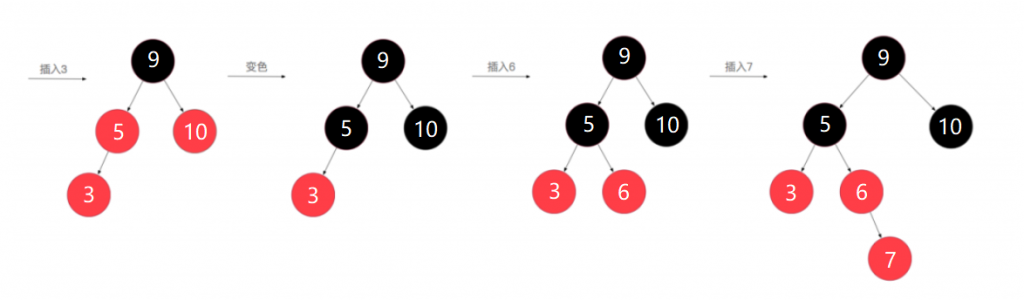
1、插入节点3后,可以看到又不符合红黑树的规则了,而此时的情况,需要采用颜色反转的操作,就是把5、10两个节点变为黑色,5、10的父节点变为红色,但父节点9是根节点,不能为红色,于是再将9变为黑色,这样整个树的深度其实增加了1层
2、继续插入6节点,对树深度没有影响
3、插入7节点后,6、7节点都为红节点,不满足规则4,需要进行颜色反转调整,也就是7的父节点和叔叔节点变为黑色,爷爷节点5变为红色
上图所示过程如下:
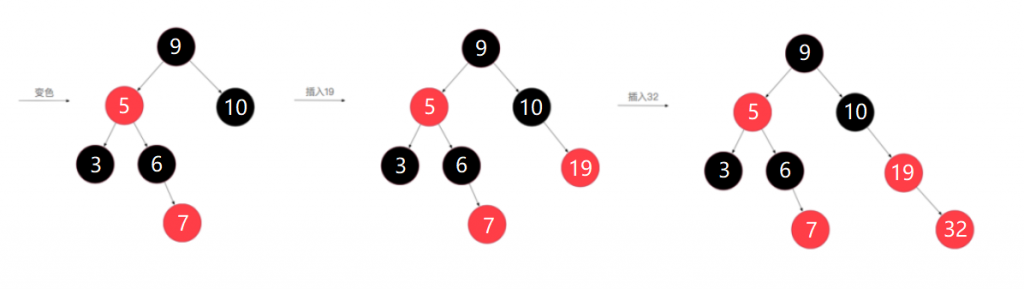
1、继续插入节点19,对树深度没有影响,红黑树的规则都满足,无需调整
2、插入节点32后,又出现了不满足规则4的情况,此时节点32没有叔叔节点,如果颜色反转的话,左右子树的深度就出现不一致的情况,所以需要对爷爷节点进行左旋操作
3、父节点取代爷爷节点的位置,父节点变为黑色,爷爷节点变为父节点的左子树变为红色
上图所示过程如下:
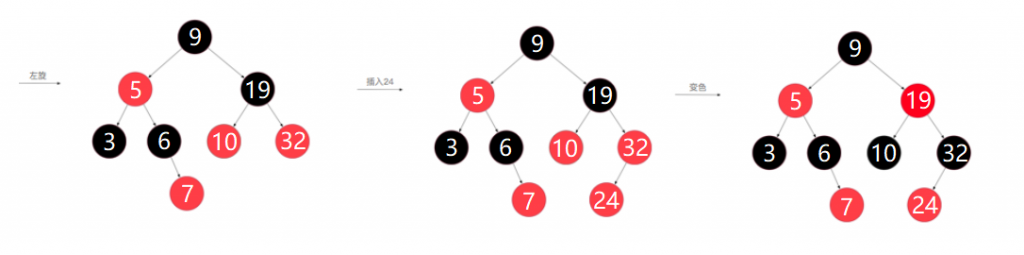
1、入节点24后,红黑树不满足规则4,需要调整
2、此时父节点32和叔叔节点10都为红色,需要进行颜色反转,爷爷节点19变为红色,父节点、叔叔节点变为黑色,颜色反转树的深度不发生变化
上图所示过程如下:
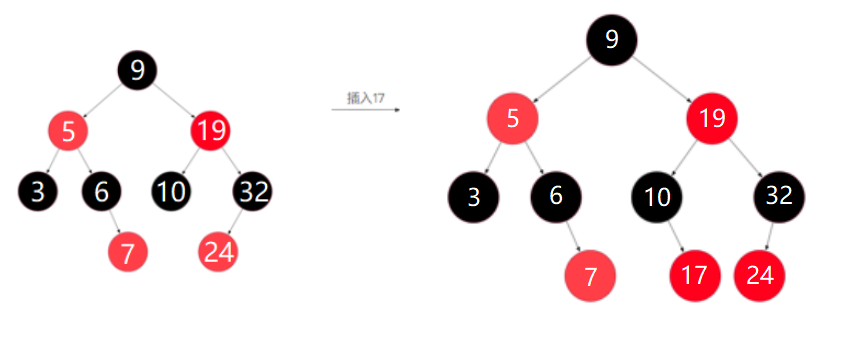
1、插入节点17后,未破坏红黑树规则,不需要调整
代码实现:
package com.rubin.datastructure.tree;
import lombok.Getter;
import lombok.Setter;
@Getter
@Setter
public class RubinRedBlackNode {
private int value;
private boolean isBlack;
private RubinRedBlackNode left;
private RubinRedBlackNode right;
private RubinRedBlackNode parent;
public RubinRedBlackNode(int value) {
this.value = value;
this.isBlack = false;
}
@Override
public String toString() {
return "{" +
"\"value\":" + value +
", \"color\":" + (isBlack ? "\"black\"" : "\"red\"") +
", \"left\":" + left +
", \"right\":" + right +
'}';
}
}
package com.rubin.datastructure.tree;
/**
* 红黑树
* <p>
* 红黑树的五个规则:
* 1、每个节点要么是黑色,要么是红色
* 2、根节点是黑色
* 3、每个叶子节点都是黑色的空节点(NIL节点)(为了简单起见,一般会省略该节点)
* 4、如果一个节点是红色的,则它的子节点必须是黑色的(父子不能同为红)
* 5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(平衡的关键)
*/
public class RubinRedBlackTree {
private RubinRedBlackNode root;
public RubinRedBlackTree() {
}
/**
* 遍历打印整棵树
*/
public void list() {
doList(root);
}
private void doList(RubinRedBlackNode node) {
if (node == null) {
return;
}
doList(node.getLeft());
System.out.println(node);
doList(node.getRight());
}
/**
* 添加节点
* 红黑树会自平衡 以保持树的高度始终平衡 避免查询效率退化
* 红黑树自平衡有下列五种情况:
* 1、新节点位于树根,没有父节点。直接让新节点变色为黑色,规则2得到满足。同时,黑色的根节点使得每条路径上的黑色节点数目都增加了1,所以并没有打破规则5
* 2、新节点的父节点是黑色。新插入的红色节点B并没有打破红黑树的规则,所以不需要做任何调整
* 3、新节点的父节点和叔叔节点都是红色。这种情况要向上变色,一直到根节点,最后把根节点着色黑色
* 4、新节点的父节点是红色,叔叔节点是黑色或者没有叔叔,且新节点是父节点的右孩子(左孩子),父节点(B)是祖父节点的左孩子(右孩子)。这时需要将父节点左旋(右旋),进入情况5
* 5、新节点的父节点是红色,叔叔节点是黑色或者没有叔叔,且新节点是父节点的左孩子(右孩子),父节点(B)是祖父节点的左孩子(右孩子)。这时将父节点变为黑色,爷爷节点变为红色,
* 再将爷爷节点右旋(左旋)
*
* @param value
*/
public void insert(int value) {
RubinRedBlackNode node = new RubinRedBlackNode(value),
exsitNode;
if (root == null) {
root = node;
} else if ((exsitNode = checkNodeExist(value)) != null) {
exsitNode.setValue(value);
return;
} else {
RubinRedBlackNode parent = findParentNode(value);
if (value > parent.getValue()) {
parent.setRight(node);
} else if (value < parent.getValue()) {
parent.setLeft(node);
}
node.setParent(parent);
}
insertBalance(node);
}
/**
* 插入重平衡红黑树
*
* @param node
*/
private void insertBalance(RubinRedBlackNode node) {
RubinRedBlackNode father, grand, uncle;
boolean fatherLeft = false;
// 只考虑有父节点并且父节点是红色的情况
while ((father = node.getParent()) != null && father.isBlack() == false) {
grand = father.getParent();
// 父节点是左孩子
if (grand.getLeft() == father) {
uncle = grand.getRight();
fatherLeft = true;
}
// 父节点是右孩子
else {
uncle = grand.getLeft();
}
// 父节点以及父节点的兄弟节点均为红色 向上变色
if (uncle != null && uncle.isBlack() == false) {
setBlack(father);
setBlack(uncle);
setRed(grand);
node = grand;
continue;
}
// 父节点是左孩子
if (fatherLeft) {
// 自己是右孩子
if (father.getRight() == node) {
leftRotate(father);
RubinRedBlackNode tmp = father;
father = node;
node = tmp;
}
// 自己是左孩子
else {
setBlack(father);
setRed(grand);
rightRotate(grand);
}
}
// 父节点是右孩子
else {
// 自己是左孩子
if (father.getLeft() == node) {
rightRotate(father);
RubinRedBlackNode tmp = father;
father = node;
node = tmp;
}
// 自己是右孩子
else {
setBlack(father);
setRed(grand);
leftRotate(grand);
}
}
}
setBlack(root);
}
/**
* 左旋
*
* @param node
*/
private void leftRotate(RubinRedBlackNode node) {
RubinRedBlackNode rightChild = node.getRight(),
father = node.getParent();
if (father == null) {
root = rightChild;
rightChild.setParent(null);
} else {
rightChild.setParent(father);
if (father.getLeft() == node) {
father.setLeft(rightChild);
} else {
father.setRight(rightChild);
}
}
node.setRight(rightChild.getLeft());
if (rightChild.getLeft() != null) {
rightChild.getLeft().setParent(node);
}
rightChild.setLeft(node);
node.setParent(rightChild);
}
/**
* 右旋
*
* @param node
*/
private void rightRotate(RubinRedBlackNode node) {
RubinRedBlackNode leftChild = node.getLeft(),
father = node.getParent();
if (father == null) {
root = leftChild;
leftChild.setParent(null);
} else {
leftChild.setParent(father);
if (father.getLeft() == node) {
father.setLeft(leftChild);
} else {
father.setRight(leftChild);
}
}
node.setLeft(leftChild.getRight());
if (leftChild.getRight() != null) {
leftChild.getRight().setParent(node);
}
leftChild.setRight(node);
node.setParent(leftChild);
}
/**
* 给节点着黑色
*
* @param node
*/
private void setBlack(RubinRedBlackNode node) {
node.setBlack(true);
}
/**
* 给节点着红色
*
* @param node
*/
private void setRed(RubinRedBlackNode node) {
node.setBlack(false);
}
/**
* 查找新节点的父节点
*
* @param value
* @return
*/
private RubinRedBlackNode findParentNode(int value) {
RubinRedBlackNode parent = root, child;
if (value > parent.getValue()) {
child = parent.getRight();
} else if (value < parent.getValue()) {
child = parent.getLeft();
} else {
throw new RuntimeException("the node value: " + value + " has exsit");
}
while (child != null) {
parent = child;
if (value > parent.getValue()) {
child = parent.getRight();
} else if (value < parent.getValue()) {
child = parent.getLeft();
} else {
throw new RuntimeException("the node value: " + value + " has exsit");
}
}
return parent;
}
/**
* 查找有没有相同的节点
*
* @param value
* @return
*/
private RubinRedBlackNode checkNodeExist(int value) {
RubinRedBlackNode node = root;
while (node != null) {
if (node.getValue() == value) {
return node;
} else if (value > node.getValue()) {
node = node.getRight();
} else {
node = node.getLeft();
}
}
return null;
}
public static void main(String[] args) {
RubinRedBlackTree tree = new RubinRedBlackTree();
tree.insert(10);//根节点
tree.insert(5);
tree.insert(9);
tree.insert(3);
tree.insert(6);
tree.insert(7);
tree.insert(19);
tree.insert(32);
tree.insert(24);
tree.insert(17);
tree.list();
}
}
时间复杂度:O(logn)
应用
JDK1.8中HashMap使用数组+链表+红黑树的数据结构。内部维护着一个数组table,该数组保存着每个链表的表头节点或者树的根节点。HashMap存储数据的数组定义如下,里面存放的是Node实体:
transient Node<K, V>[] table;//序列化时不自动保存
/*** 桶的树化阈值:即 链表转成红黑树的阈值, * 在存储数据时,当链表长度 > 该值时,则将链表转换
成红黑树 */
static final int TREEIFY_THRESHOLD = 8;多路查找树
多路查找树(muitl-way search tree),其每一个节点的孩子数可以多于两个,且每一个节点处可以存储多个元素。
B树
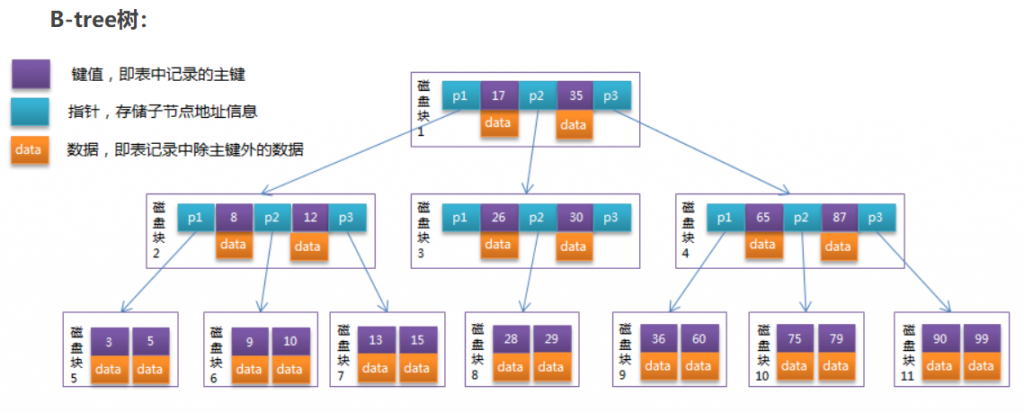
B树(BalanceTree)是对二叉查找树的改进。它的设计思想是,将相关数据尽量集中在一起,以便一次读取多个数据,减少硬盘操作次数。
一棵m阶的B 树 (m叉树)的特性如下:
- B树中所有节点的孩子节点数中的最大值称为B树的阶,记为M
- 树中的每个节点至多有M棵子树 ---即:如果定了M,则这个B树中任何节点的子节点数量都不能超过M
- 若根节点不是终端节点,则至少有两棵子树
- 除根节点和叶节点外,所有点至少有m/2棵子树
- 所有的叶子节点都位于同一层
B+树
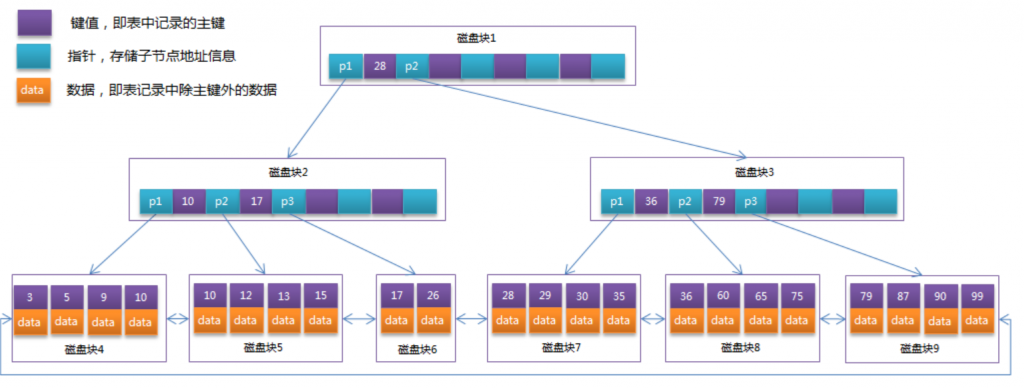
B+树是B-树的变体,也是一种多路搜索树,其定义基本与B树相同,它的自身特征是:
- 非叶子节点的子树指针与关键字个数相同
- 非叶子节点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
- 为所有叶子节点增加一个链指针
- 所有关键字都在叶子节点出现
典型应用
MySQL索引B+Tree。
B树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树:
- B树的高度一般都是在2-4这个高度,树的高度直接影响IO读写的次数
- 如果是三层树结构---支撑的数据可以达到20G,如果是四层树结构---支撑的数据可以达到几十T
B和B+的区别
B树和B+树的最大区别在于非叶子节点是否存储数据的问题,B树是非叶子节点和叶子节点都会存储数据,B+树只有叶子节点才会存储数据,而且存储的数据都是在一行上,而且这些数据都是有指针指向的,也就是有顺序的。
二叉堆
二叉堆本质上是一种完全二叉树,它分为两个类型:
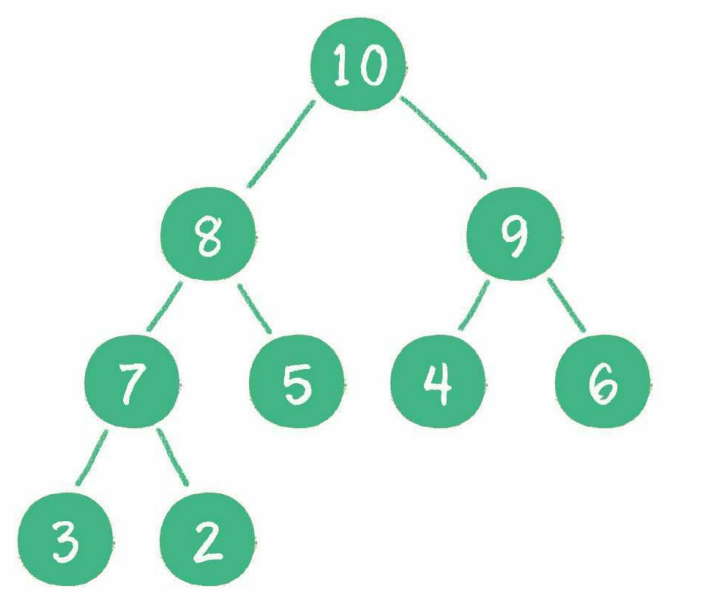
- 大顶堆(最大堆)
最大堆的任何一个父节点的值,都大于或等于它左、右孩子节点的值。
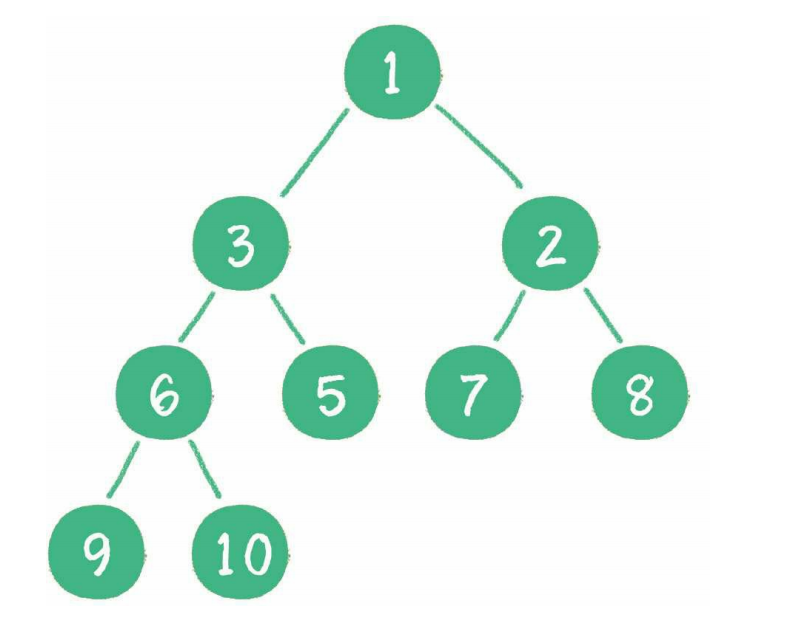
- 小顶堆(最小堆)
最小堆的任何一个父节点的值,都小于或等于它左、右孩子节点的值。
二叉堆的根节点叫作堆顶。
最大堆和最小堆的特点决定了:最大堆的堆顶是整个堆中的最大元素;最小堆的堆顶是整个堆中的最小元素。
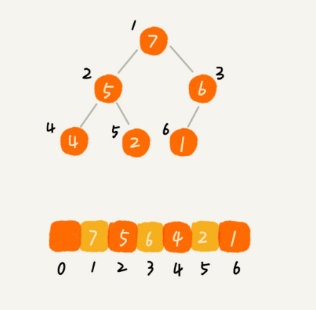
二叉堆的存储原理
完全二叉树比较适合用数组来存储。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
从图中我们可以看到,数组中下标为 i 的节点的左子节点,就是下标为 i∗2 的节点,右子节点就是下标为 i∗2+1 的节点,父节点就是下标为 i/2 取整的节点
二叉堆的典型应用
优先队列
利用堆求 Top K问题
在一个包含 n 个数据的数组中,我们可以维护一个大小为 K 的小顶堆,顺序遍历数组,从数组中取出数据与堆顶元素比较。如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;如果比堆顶元素小,则不做处理,继续遍历数组。这样等数组中的数据都遍历完之后,堆中的数据就是前 K 大数据了。
以上就是本文的全部内容了。欢迎小伙伴们积极留言交流~~~
文章评论