贪心算法
概念
贪婪算法(Greedy)的定义:是一种在每一步选中都采取在当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法
由于贪心算法的高效性以及所求得答案比较接近最优结果,贪心算法可以作为辅助算法或解决一些要求结果不特别精确的问题
注意:当下是最优的,并不一定全局是最优的。举例如下:
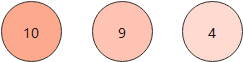
有硬币分值为10、9、4若干枚,问如果组成分值18,最少需要多少枚硬币?
采用贪心算法,选择当下硬币分值最大的:10
18-10=8
8/4=2
即:1个10、2个4,共需要3枚硬币
实际上我们知道,选择分值为9的硬币,2枚就够了
18/9=2
如果改成:
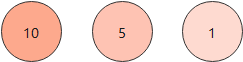
有硬币分值为10、5、1若干枚,问如果组成分值16,最少需要多少枚硬币?
采用贪心算法,选择当下硬币分值最大的:10
16-10=6
6-5=1
即:1个10,1个5,1个1 ,共需要3枚硬币
即为最优解
由此可以看出贪心算法适合于一些特殊的情况,如果能用一定是最优解
经典问题:部分背包
背包问题是算法的经典问题,分为部分背包和0-1背包,主要区别如下:
部分背包:某件物品是一堆,可以带走其一部分
0-1背包:对于某件物品,要么被带走(选择了它),要么不被带走(没有选择它),不存在只带走一部分的情况
部分背包问题可以用贪心算法求解,且能够得到最优解
假设一共有N件物品,第 i 件物品的价值为 Vi ,重量为Wi,一个小偷有一个最多只能装下重量为W的背包,他希望带走的物品越有价值越好,可以带走某件物品的一部分,请问:他应该选择哪些物品?
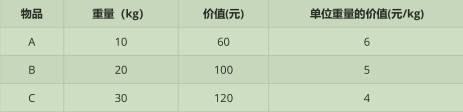
假设背包可容纳50Kg的重量,物品信息如下表:
贪心算法的关键是贪心策略的选择
将物品按单位重量 所具有的价值排序。总是优先选择单位重量下价值最大的物品
按照我们的贪心策略,单位重量的价值排序: 物品A > 物品B > 物品C
因此,我们尽可能地多拿物品A,直到将物品1拿完之后,才去拿物品B,然后是物品C 可以只拿一部分…..
package com.rubin.algorithm.greedy;
public class Goods {
private String name; //名称
private double weight; //重量
private double price; //价格
private double value; //价值
public Goods(String name, double weight, double price) {
this.name = name;
this.weight = weight;
this.price = price;
this.value=price/weight;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public double getWeight() {
return weight;
}
public void setWeight(double weight) {
this.weight = weight;
}
public double getPrice() {
return price;
}
public void setPrice(double price) {
this.price = price;
}
public double getValue() {
return value;
}
public void setValue(double value) {
this.value = value;
}
}
package com.rubin.algorithm.greedy;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
import java.util.stream.Collectors;
/**
* 背包问题
* 贪心算法实现
*
* 在不考虑排序的前提下,贪心算法只需要一次循环,所以时间复杂度是O(n)
*
* 优点:性能高,能用贪心算法解决的往往是最优解
* 缺点:在实际情况下能用的不多,用贪心算法解的往往不是最好的
*/
public class Bag {
private double maxWeight;
public Bag(double maxWeight) {
this.maxWeight = maxWeight;
}
public void take(List<Goods> goods) {
goods = goods.stream().sorted(Comparator.comparingDouble(Goods::getValue).reversed()).collect(Collectors.toList());
double sumWeight = 0.00;
for (Goods good : goods) {
sumWeight += good.getWeight();
if (sumWeight < maxWeight) {
System.out.println(good.getName() + "取" + good.getWeight() + "kg");
} else {
System.out.println(good.getName() + "取" + (good.getWeight() - sumWeight + maxWeight) + "kg");
return;
}
}
}
public static void main(String[] args) {
Bag bag = new Bag(50);
Goods g1 = new Goods("A", 10, 60); //6
Goods g2 = new Goods("B", 20, 100); //5
Goods g3 = new Goods("C", 30, 120); //4
Goods[] goods = {g1, g2, g3}; // 价值倒序
bag.take(Arrays.asList(goods));
}
}
时间复杂度
在不考虑排序的前提下,贪心算法只需要一次循环,所以时间复杂度是O(n)
优缺点
优点:性能高,能用贪心算法解决的往往是最优解
缺点:在实际情况下能用的不多,用贪心算法解的往往不是最好的
适用场景
针对一组数据,我们定义了限制值和期望值,希望从中选出几个数据,在满足限制值的情况下,期望值最大
每次选择当前情况下,在对限制值同等贡献量的情况下,对期望值贡献最大的数据(局部最优而全局最优)
大部分能用贪心算法解决的问题,贪心算法的正确性都是显而易见的,也不需要严格的数学推导证明
在实际情况下,用贪心算法解决问题的思路,并不总能给出最优解
分治算法
概念
分治算法(divide and conquer)的核心思想其实就是四个字,分而治之 ,也就是将原问题划分成 n个规模较小,并且结构与原问题相似的子问题,递归地解决这些子问题,然后再合并其结果,就得到原问题的解
关于分治和递归的区别:分治算法是一种处理问题的思想,递归是一种编程技巧
分治算法的递归实现中,每一层递归都会涉及这样三个操作:
- 分解:将原问题分解成一系列子问题
- 解决:递归地求解各个子问题,若子问题足够小,则直接求解
- 合并:将子问题的结果合并成原问题
比如:
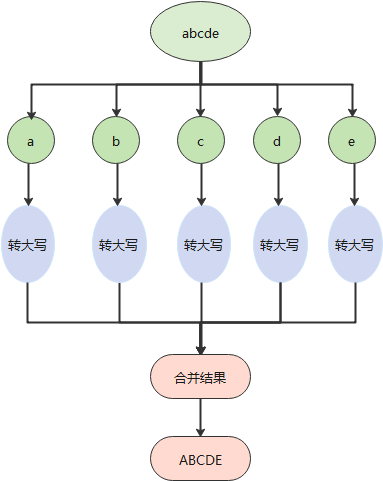
将字符串中的小写字母转化为大写字母
“abcde”转化为"ABCDE"
我们可以利用分治的思想将整个字符串转化成一个一个的字符处理
经典问题
求X的n次幂的问题,比如:
2^10 2的10次幂
一般的解法是循环10次
public static int commpow(int x,int n){
int s=1;
while(n>=1){
s*=x;
n--;
}
return s;
}该方法的时间复杂度是:O(n)
采用分治法
package com.rubin.algorithm.ra;
/**
* 求x的n次方
* 使用分治算法来算
* T = O(logn)
*/
public class HalfPow {
public static int halfPow(int x, int n) {
if (n == 1) {
return x;
}
int half = halfPow(x, n / 2);
if (n % 2 == 0) {
return half * half;
} else {
return half * half * x;
}
}
public static void main(String[] args) {
System.out.println(halfPow(5, 4));
}
}
时间复杂度
根据拆分情况可以是O(n)或O(logn)
优缺点
优势:将复杂的问题拆分成简单的子问题,解决更容易,另外根据拆分规则,性能有可能提高
劣势:子问题必须要一样,用相同的方式解决
适用场景
分治算法能解决的问题,一般需要满足下面这几个条件:
- 原问题与分解成的小问题具有相同的模式
- 原问题分解成的子问题可以独立求解,子问题之间没有相关性,这一点是分治算法跟动态规划的明显区别
- 具有分解终止条件,也就是说,当问题足够小时,可以直接求解
- 可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了
回溯算法
概念
回溯算法实际上一个类似枚举的深度优先搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回(也就是递归返回),尝试别的路径
回溯的处理思想,有点类似枚举(列出所有的情况)搜索。我们枚举所有的解,找到满足期望的解。为了有规律地枚举所有可能的解,避免遗漏和重复,我们把问题求解的过程分为多个阶段。每个阶段,我们都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走
经典问题
N皇后问题
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击
我们把这个问题划分成 8 个阶段,依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中,我们不停地检查当前放法,是否满足要求。如果满足,则跳到下一行继续放置棋子;如果不满足,那就再换一种放法,继续尝试
代码如下:
package com.rubin.algorithm.back;
/**
* n皇后问题
* <p>
* 使用回溯算法
*/
public class NQueen {
private static final int QUEENS = 8;
//下标表示行,值表示queen存储在哪一列
private static final int[] result = new int[QUEENS];
public static void setQueens(int row) {
if (row >= QUEENS) {
print();
return;
}
for (int col = 0; col < QUEENS; col++) {
if (isOK(row, col)) {
result[row] = col;
setQueens(row + 1);
}
}
}
/**
* 判断是否OK的标准 同一行上方、左上角、右下角不能有皇后
*
* @param row
* @param col
* @return
*/
private static boolean isOK(int row, int col) {
int leftup = col - 1;//左对角线
int rightup = col + 1;//右对角线
for (int i = row - 1; i >= 0 ; i--) {
if (result[i] == col) {
return false;
}
if (leftup >= 0) {
if (result[i] == leftup) {
return false;
}
}
if (rightup < QUEENS) {
if (result[i] == rightup) {
return false;
}
}
leftup--;
rightup++;
}
return true;
}
private static void print() {
for (int i = 0; i < result.length; i++) {
for (int j = 0; j < result.length; j++) {
if (result[i] == j) {
System.out.print("Q|");
} else {
System.out.print("*| ");
}
}
System.out.println();
}
System.out.println("-------------------");
}
public static void main(String[] args) {
setQueens(0);
}
}
时间复杂度
N皇后问题的时间复杂度为:O(n!) 实际为 n!/2
优缺点
优点:回溯算法的思想非常简单,大部分情况下,都是用来解决广义的搜索问题,也就是,从一组可能的解中,选择出一个满足要求的解。回溯算法非常适合用递归来实现,在实现的过程中,剪枝操作是提高回溯效率的一种技巧。利用剪枝,我们并不需要穷举搜索所有的情况,从而提高搜索效率
劣势:效率相对于低
适用场景
回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题,我们都可以用回溯算法解决。回溯算法相当于穷举搜索。穷举所有的情况,然后对比得到最优解。不过,回溯算法的时间复杂度非常高,是指数级别的,只能用来解决小规模数据的问题。对于大规模数据的问题,用回溯算法解决的执行效率就很低了
动态规划
概念
动态规划(Dynamic Programming),是一种分阶段求解的方法
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决
首先是拆分问题,我的理解就是根据问题的可能性把问题划分成一步一步,这样就可以通过递推或者递归来实现。关键就是这个步骤,动态规划有一类问题就是从后往前推导。有时候我们很容易知道:如果只有一种情况时,最佳的选择应该怎么做,然后根据这个最佳选择往前一步推导,得到前一步的最佳选择,然后就是定义问题状态和状态之间的关系。我的理解是前面拆分的步骤之间的关系,用一种量化的形式表现出来,类似于高中学的推导公式,因为这种式子很容易用程序写出来,也可以说对程序比较亲和(也就是最后所说的状态转移方程式) 。我们再来看定义的下面的两段,我的理解是比如我们找到最优解,我们应该将最优解保存下来,为了往前推导时能够使用前一步的最优解,在这个过程中难免有一些相比于最优解差的解,此时我们应该放弃,只保存最优解,这样我们每一次都把最优解保存了下来,大大降低了时间复杂度
动态规划中有三个重要概念:
- 最优子结构
- 边界
- 状态转移公式(递推方程)dp方程
经典问题
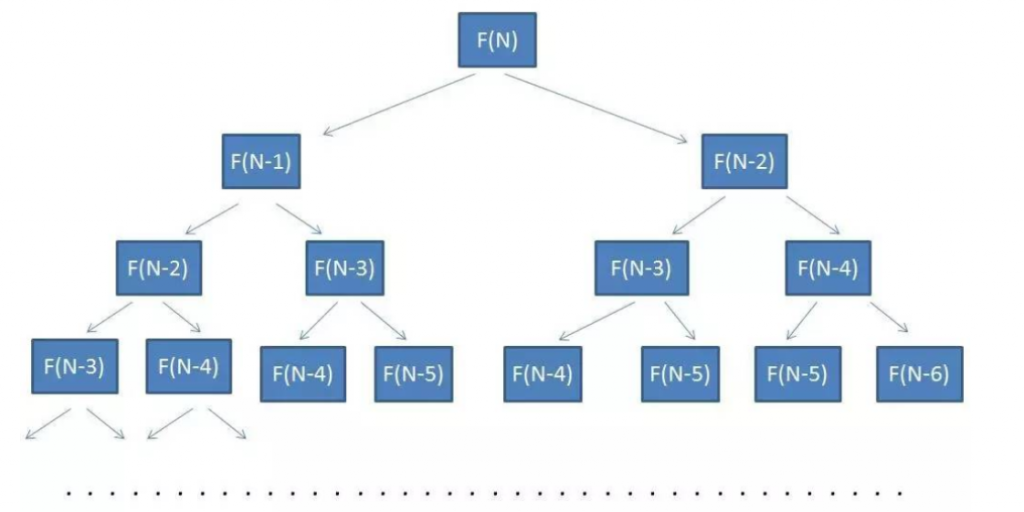
再谈斐波那契数列
优化递归:
通过上边的递归树可以看出在树的每层和上层都有大量的重复计算,可以把计算结果存起来,下次再用的时候就不用再计算了,这种方式叫记忆搜索,也叫做备忘录模式
代码如下:
package com.rubin.algorithm.dp;
/**
* 优化版本 使用备忘录模式
*/
public class FibonacciRecord {
private static final int[] records = new int[20];
public static int findFibonacciItem(int index) {
if (index <= 1) {
return index;
}
if (records[index] == 0) {
records[index] = findFibonacciItem(index -1) + findFibonacciItem(index - 2);
}
return records[index];
}
public static void main(String[] args) {
for (int i = 0; i < 10; i++) {
System.out.print(findFibonacciItem(i) + " ");
}
}
}
dp方程:
if(i < 2) 则
dp[0] = 0, dp[1] = 1
if(i >= 2) 则
dp[i] = dp[i - 1] + dp[i - 2]
最优子结构: fib[9]=finb[8]+fib[7]
边界:a[0]=0; a[1]=1
dp方程:fib[n]=fib[n-1]+fib[n-2]
实现代码如下:
package com.rubin.algorithm.dp;
/**
* 优化版本 使用方程递推模式
* T = O(n)
*/
public class FibonacciFunction {
public static int findFibonacciItem(int index) {
int[] records = new int[index + 1];
records[0] = 0;
records[1] = 1;
for (int i = 2; i <= index; i++) {
records[i] = records[i-1] + records[i-2];
}
return records[index - 1];
}
public static void main(String[] args) {
for (int i = 1; i <= 10; i++) {
System.out.print(findFibonacciItem(i) + " ");
}
}
}
0-1背包问题
有n件物品和一个最大承重为W的背包,每件物品的重量是w[i],价值是v[i]
在保证总重量不超过W的前提下,选择某些物品装入背包,背包的最大总价值是多少?
注意:每个物品只有一件,也就是每个物品只能选择0件或者1件
分析:
假设:W=10,有5件物品,重量和价值如下:
w[1]=2,v[1]=6
w[2]=2,v[2]=3
w[3]=6,v[3]=5
w[4]=5,v[4]=4
w[5]=4,v[5]=6
dp数组的计算结果如下表:
i:选择i件物品 j:最大承重
解法:
dp方程:
如果:
可以选这一件物品
j < w[i]
不选:
dp[i, j] = dp[i - 1, j]
选了:
dp[i, j] = v[i] + dp[i - 1, j - w[i]]
两者取价值最大的数:Max( dp[i - 1, j] , v[i] + dp[i - 1, j - w[i]] )
不可以选这件物品:
j < w[i] 则:
dp[i, j] = dp[i - 1, j]
代码如下:
package com.rubin.algorithm.dp;
/**
* 0-1背包问题
* 有n件物品和一个最大承重为W的背包,每件物品的重量是w[i],价值是v[i],在保证总重量不超过W的前提下,选择某些物品装入背包,背包的最大总价值是多少?
* 注意:每个物品只有一件,也就是每个物品只能选择0件或者1件
* <p>
* 分析:
* 假设:W=10,有5件物品,重量和价值如下:
* w[1]=2,v[1]=6
* w[2]=2,v[2]=3
* w[3]=6,v[3]=5
* w[4]=5,v[4]=4
* w[5]=4,v[5]=6
* dp数组的计算结果如下表:
* i\j 0 1 2 3 4 5 6 7 8 9 10
* 0 0 0 0 0 0 0 0 0 0 0 0
* 1 (w[1]=2,v[1]=6) 0 0 6 6 6 6 6 6 6 6 6
* 2(w[2]=2,v[2]=3) 0 0 6 6 9 9 9 9 9 9 9
* 3(w[3]=6,v[3]=5) 0 0 6 6 9 9 9 9 11 11 14
* 4(w[4]=5,v[4]=4) 0 0 6 6 9 9 9 10 11 13 14
* 5(w[5]=4,v[5]=6) 0 0 6 6 9 9 12 12 15 15 15
* i:选择i件物品 j:最大承重
*
* T = O(i*j)
*/
public class BagDP {
public static int maxValue(int[] values, int[] weights, int max) {
if (values == null || weights == null || max <= 0 || values.length == 0 || weights.length == 0) {
return 0;
}
int[][] DP = new int[values.length + 1][max + 1];
for (int i = 1; i <= values.length; i++) {
for (int j = 1; j <= max; j++) {
if (j < weights[i - 1]) {
DP[i][j] = DP[i - 1][j];
} else {
DP[i][j] = Math.max(DP[i - 1][j], values[i - 1] + DP[i - 1][j - weights[i - 1]]);
}
}
}
int maxValue = DP[values.length][max];
int j = max;
for (int i = values.length; i > 0; i--) {
if (DP[i][j] > DP[i - 1][j]) {
System.out.println("选择了:w=" + weights[i - 1] + ",v=" + values[i - 1]);
j -= weights[i - 1];
if (j <= 0) {
break;
}
}
}
return maxValue;
}
public static void main(String[] args) {
int[] values = {60, 30, 50, 40, 60};
int[] weights = {2, 2, 6, 5, 4};
int max = 10;
System.out.println("最大价值是:" + maxValue(values, weights, max));
}
}
此种解法时间复杂度为O(i * j)
使用动态规划四个步骤
- 把当前的复杂问题转化成一个个简单的子问题(分治)
- 寻找子问题的最优解法(最优子结构)
- 把子问题的解合并,存储中间状态
- 递归+记忆搜索或自底而上的形成递推方程(dp方程)
时间复杂度
新的斐波那契数列实现时间复杂度为O(n)
优缺点
优点:时间复杂度和空间复杂度都相当较低
缺点:难,有些场景不适用
适用场景
尽管动态规划比回溯算法高效,但是,并不是所有问题,都可以用动态规划来解决。能用动态规划解决的问题,需要满足三个特征,最优子结构、无后效性和重复子问题。在重复子问题这一点上,动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题,不能有重复子问题,而动态规划正好相反,动态规划之所以高效,就是因为回溯算法实现中存在大量的重复子问题
环形链表问题
给定一个链表,判断链表中是否有环。存在环返回 true ,否则返回 false
解法:
1、定义快慢两个指针:slow=head; fast=head.next;
2、遍历链表:快指针步长为2:fast=fast.next.next; 慢指针步长为1:slow=slow.next;
3、当且仅当快慢指针重合(slow==fast),有环,返回true
4、快指针为null,或其next指向null,没有环,返回false,操作结束
代码实现:
package com.rubin.algorithm.ring;
/**
* 链表节点
*/
public class Node {
int id;
String name;
Node next;
public Node(int id, String name) {
this.id = id;
this.name = name;
}
}
package com.rubin.algorithm.ring;
/**
* 判断链表是否有环
*/
public class RingList {
/**
* 判断链表是否有环
* @param head
* @return
*/
public static boolean isRing(Node head){
if(head==null) return false;
//定义快慢指针
Node slow=head; //慢
Node fast=head.next; //快
while(fast!=null&&fast.next!=null){
//追击相遇 有环
if(slow==fast){
return true;
}
fast=fast.next.next; //步长为2
slow=slow.next;//步长为1
}
//无环
return false;
}
public static void main(String[] args) {
Node n1=new Node(1,"张飞");
Node n2=new Node(2,"赵云");
Node n3=new Node(3,"关羽");
Node n4=new Node(4,"黄忠");
Node n5=new Node(5,"狄仁杰");
n1.next=n2;
n2.next=n3;
n3.next=n4;
n4.next=n5;
n5.next=n1;
System.out.println(isRing(n1));
}
}
以上就是本文的全部内容。欢迎小伙伴们积极留言交流~~~



文章评论